题目内容
已知三条直线a,b,c和平面β,则下列推论中正确的是( )
| A、若a∥b,b?β,则a∥β |
| B、若a∥β,b∥β,则a∥b或a与b相交 |
| C、若a⊥c,b⊥c,则a∥b |
| D、若a?β,b∥β,a,b共面,则a∥b |
考点:空间中直线与平面之间的位置关系
专题:探究型,空间位置关系与距离
分析:观察题设条件以及四个选项,A选项研究线面平行的问题用线面平行的条件进行判断,B,C,D三个选项研究线线平行的问题,用线线平行的条件进行判断,
解答:
解:A选项不正确,由于不能保证a不在面内,故无法判断线面平行;
B选项,a∥β,b∥β,则a∥b或a与b相交或异面;
C选项不正确,垂直于同一条直线的两个直线的位置关系可能是平行,相交,异面,故不正确;
D选项正确,此是线面平行的性质定理的内容,故正确.
故选:D.
B选项,a∥β,b∥β,则a∥b或a与b相交或异面;
C选项不正确,垂直于同一条直线的两个直线的位置关系可能是平行,相交,异面,故不正确;
D选项正确,此是线面平行的性质定理的内容,故正确.
故选:D.
点评:本题考查空间中直线与平面之间的位置关系,求解此类题关键是熟练掌握了空间中线面之间位置关系的特征及有较好的空间想像能力.

练习册系列答案
相关题目
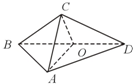 在三棱锥C-ABD中(如图),△ABD与△CBD是全等的等腰直角三角形,O为斜边BD的中点,AB=4,二面角A-BD-C的大小为60°,并给出下面结论:
在三棱锥C-ABD中(如图),△ABD与△CBD是全等的等腰直角三角形,O为斜边BD的中点,AB=4,二面角A-BD-C的大小为60°,并给出下面结论:①AC⊥BD;
②AD⊥CO;
③△AOC为正三角形;
④cos∠ADC=
| ||
| 4 |
⑤四面体ABCD的外接球面积为32π.
其中真命题是( )
| A、②③④ | B、①③④ |
| C、①④⑤ | D、①③⑤ |
不等式x(x-3)<0的解集是( )
| A、{x|x<0} |
| B、{x|x<3} |
| C、{x|0<x<3} |
| D、{x|x<0或x>3} |
若函数f(x)=
(a∈R)是奇函数,则a的值为( )
| x+a |
| x2+1 |
| A、1 | B、0 | C、-1 | D、±1 |
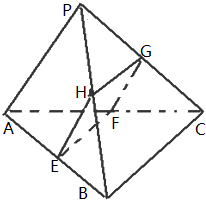 如图,已知点P是三角形ABC所在平面外一点,且PA=BC=1,截面EFGH分别平行于PA,BC(点E,F,G,H分在棱AB,AC,PC,PB上)
如图,已知点P是三角形ABC所在平面外一点,且PA=BC=1,截面EFGH分别平行于PA,BC(点E,F,G,H分在棱AB,AC,PC,PB上)