题目内容
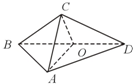 在三棱锥C-ABD中(如图),△ABD与△CBD是全等的等腰直角三角形,O为斜边BD的中点,AB=4,二面角A-BD-C的大小为60°,并给出下面结论:
在三棱锥C-ABD中(如图),△ABD与△CBD是全等的等腰直角三角形,O为斜边BD的中点,AB=4,二面角A-BD-C的大小为60°,并给出下面结论:①AC⊥BD;
②AD⊥CO;
③△AOC为正三角形;
④cos∠ADC=
| ||
| 4 |
⑤四面体ABCD的外接球面积为32π.
其中真命题是( )
| A、②③④ | B、①③④ |
| C、①④⑤ | D、①③⑤ |
考点:棱锥的结构特征
专题:空间位置关系与距离
分析:根据等腰直角三角形的性质得OA⊥BD,OC⊥BD,且OC=OA=OB=OD=
BD,再由线面垂直的判定定理判断出①、②、③的正确性;由余弦定理求出cos∠ADC的值判断出④正确性;再由条件求出四面体ABCD的外接球的半径,求出它的表面积判断出⑤正确性.
| 1 |
| 2 |
解答:
解:∵△ABD与△CBD是全等的等腰直角三角形,O为斜边BD的中点,
∴OA⊥BD,OC⊥BD,且OC=OA=
BD,
又∵0A∩OC=O,∴BD⊥平面AOC,
则AC⊥BD,即①正确;
由二面角A-BD-C的大小为60°得,∠AOC=60°,
∵OC=OA,∴△AOC为正三角形,即③正确;
假设AD⊥CO,由OC⊥BD,且AD∩BD=D得,OC⊥平面ABD,
∴0A⊥OC,这与∠AOC=60°矛盾,故②不正确;
由AB=4得,AD=CD=4,且AC=OC=OA=2
,
∴cos∠ADC=
=
=
,
故④不正确;
由OA=OB=OC=OD得,四面体ABCD的外接球的球心是O,且半径r=2
,
∴四面体ABCD的外接球的面积为32π,故⑤正确,
故选D.
∴OA⊥BD,OC⊥BD,且OC=OA=
| 1 |
| 2 |
又∵0A∩OC=O,∴BD⊥平面AOC,
则AC⊥BD,即①正确;
由二面角A-BD-C的大小为60°得,∠AOC=60°,
∵OC=OA,∴△AOC为正三角形,即③正确;
假设AD⊥CO,由OC⊥BD,且AD∩BD=D得,OC⊥平面ABD,
∴0A⊥OC,这与∠AOC=60°矛盾,故②不正确;
由AB=4得,AD=CD=4,且AC=OC=OA=2
| 2 |
∴cos∠ADC=
| AD2+CD2-AC2 |
| 2AD•CD |
42+42-(2
| ||
| 2×4×4 |
| 3 |
| 4 |
故④不正确;
由OA=OB=OC=OD得,四面体ABCD的外接球的球心是O,且半径r=2
| 2 |
∴四面体ABCD的外接球的面积为32π,故⑤正确,
故选D.
点评:本题是以三棱锥为载体,考查了等腰直角三角形的性质、线面垂直的判定定理、二面角的定义、余弦定理和四面体的外接球的如何确定球心和求半径等,综合性强,考查了的知识点多,难度较大.

练习册系列答案
 阅读快车系列答案
阅读快车系列答案
相关题目
半径为R的球面上有A、B两点,它们的球面距离是
R,则线段AB的长为( )
| π |
| 2 |
A、
| ||||
| B、R | ||||
C、
| ||||
D、
|
已知三条直线a,b,c和平面β,则下列推论中正确的是( )
| A、若a∥b,b?β,则a∥β |
| B、若a∥β,b∥β,则a∥b或a与b相交 |
| C、若a⊥c,b⊥c,则a∥b |
| D、若a?β,b∥β,a,b共面,则a∥b |
按如图程序框图来计算,若输入x=10,则运算的次数为( )

| A、6 | B、5 | C、4 | D、3 |
