题目内容
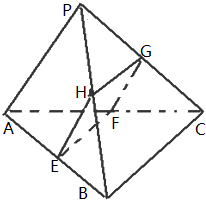如图，已知点P是三角形ABC所在平面外一点，且PA=BC=1，截面EFGH分别平行于PA，BC（点E，F，G，H分在棱AB，AC，PC，PB上）（1）求证：四边形EFGH是平行四边形且周长为定值；
（2）设PA与BC所成角为θ，求四边形EFGH的面积的最大值．
考点：棱锥的结构特征
专题：空间位置关系与距离
分析：（1）利用线面平行的判定与性质，证出EF∥GH且EH∥FG，从而得到四边形EGFH的两组对边分别平行，即四边形EFGH为平行四边形，再由平行得对应边比例，利用整体求值求出EF+EH=1，进而求出四边形EFGH的周长为定值；
（2）由异面直线所成角的定义求出∠HEF，利用正弦定理的面积公式得到截面EFGH的面积S，再利用平行线分线段成比例定理和基本不等式，得到当且仅当E为AB的中点时取到最大值．由此即可算出截面EFGH的面积最大值．
（2）由异面直线所成角的定义求出∠HEF，利用正弦定理的面积公式得到截面EFGH的面积S，再利用平行线分线段成比例定理和基本不等式，得到当且仅当E为AB的中点时取到最大值．由此即可算出截面EFGH的面积最大值．
解答：
（1）证明：∵PA∥平面EFGH，PA?平面PAB，平面PAB∩平面EFGH=EH
∴PA∥EH．同理可得PA∥GF，可得EH∥GF，
同理得到EF∥HG，
∴四边形EGFH中，两组对边分别平行，
因此，四边形EFGH为平行四边形．
∵空间四边形ABCD被一平面所截，截面EFGH是平行四边形．
且PA=BC=1，
∴
=
①，
=
②，
则①+②得，
+
=
=1
∵PA=BC=1，∴EF+EH=1，
∴四边形EFGH的周长=2，故四边形EFGH的周长为定值．
2）∵PA与BC所成角为θ，
∴平行四边形EFGH中∠HEF=θ或180°-θ，
可得截面EFGH的面积S=HE•EF•sin∠EGE=HE•EF•sinθ，
设
=
=λ，则
=
=1-λ，
∴EH=λPA=λ，同理可得EF=1-λ，且0＜λ＜1，
则S=λ（1-λ）sinθ≤(
)2sinθ=
sinθ，
当且仅当λ=
等号成立，
由此可得：当E为AB的中点时，截面EFGH的面积最大，最大值为
sinθ．
∴PA∥EH．同理可得PA∥GF，可得EH∥GF，
同理得到EF∥HG，
∴四边形EGFH中，两组对边分别平行，
因此，四边形EFGH为平行四边形．
∵空间四边形ABCD被一平面所截，截面EFGH是平行四边形．
且PA=BC=1，
∴
| EH |
| AP |
| EB |
| AB |
| EF |
| BC |
| AE |
| AB |
则①+②得，
| EH |
| AP |
| EF |
| BC |
| EB+AE |
| AB |
∵PA=BC=1，∴EF+EH=1，
∴四边形EFGH的周长=2，故四边形EFGH的周长为定值．
2）∵PA与BC所成角为θ，
∴平行四边形EFGH中∠HEF=θ或180°-θ，
可得截面EFGH的面积S=HE•EF•sin∠EGE=HE•EF•sinθ，
设
| EH |
| AP |
| EB |
| AB |
| EF |
| BC |
| AE |
| AB |
∴EH=λPA=λ，同理可得EF=1-λ，且0＜λ＜1，
则S=λ（1-λ）sinθ≤(
| λ+1-λ |
| 2 |
| 1 |
| 4 |
当且仅当λ=
| 1 |
| 2 |
由此可得：当E为AB的中点时，截面EFGH的面积最大，最大值为
| 1 |
| 4 |
点评：本题主要考查了线面平行的判定与性质、平行线分线段成比例定理和基本不等式求最值等知识，属于中档题．
练习册系列答案
阅读快车系列答案
相关题目
已知三条直线a，b，c和平面β，则下列推论中正确的是（ ）
| A、若a∥b，b?β，则a∥β |
| B、若a∥β，b∥β，则a∥b或a与b相交 |
| C、若a⊥c，b⊥c，则a∥b |
| D、若a?β，b∥β，a，b共面，则a∥b |