题目内容
一支田径队有男运动员28人，女运动员21人，现按性别用分层抽样的方法，从中抽取14位运动员进行健康检查，则男运动员应抽取 人．
考点：分层抽样方法
专题：概率与统计
分析：有男运动员28人，女运动员21人，知总体个数是20+10，从全体队员中抽出一个容量为14人的样本，得到每个个体被抽到的概率是
，得到男运动员应抽的人数是用概率乘以男运动员人数．
| 14 |
| 49 |
解答：
解：∵有男运动员28人，女运动员21人，
∴总体个数是29+21=49，
∵从全体队员中抽出一个容量为14人的样本
∴每个个体被抽到的概率是
=
∴男运动员应抽
×28=8；
故答案为：8．
∴总体个数是29+21=49，
∵从全体队员中抽出一个容量为14人的样本
∴每个个体被抽到的概率是
| 14 |
| 49 |
| 2 |
| 7 |
∴男运动员应抽
| 2 |
| 7 |
故答案为：8．
点评：本题是一个分层抽样，在抽样过程中每个个体被抽到的概率是相等的，这是一个基础题，若出现在高考题中，一定是一个必得分的题目．
练习册系列答案
天天向上一本好卷系列答案
小学生10分钟应用题系列答案
相关题目
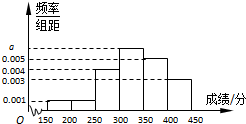某地区教育主管部门为了对该地区模拟考试成绩进行分析，随机抽取了150分到450分之间的1000名学生的成绩，并根据这1000名学生的成绩画出样本的频率分布直方图（如图），则成绩在[300，350）内的学生人数共有已知三条直线a，b，c和平面β，则下列推论中正确的是（ ）
| A、若a∥b，b?β，则a∥β |
| B、若a∥β，b∥β，则a∥b或a与b相交 |
| C、若a⊥c，b⊥c，则a∥b |
| D、若a?β，b∥β，a，b共面，则a∥b |
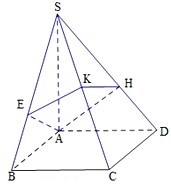如图，四棱锥S-ABCD的底面是正方形，侧棱SA⊥底面ABCD，过A作AE垂直SB交SB于E点，作AH垂直SD交SD于H点，平面AEH交SC于K点，P是SA上的动点，且AB=1，SA=2．