题目内容
设函数f(x)=lg
(a∈R)
(1)已知函数F(x)=2f(x)-f(2x)有两个不同的零点,求a的取值范围;
(2)若函数f(x)在定义域x∈(-∞,1]上有意义,求a的取值范围.
| 1+2xa |
| 2 |
(1)已知函数F(x)=2f(x)-f(2x)有两个不同的零点,求a的取值范围;
(2)若函数f(x)在定义域x∈(-∞,1]上有意义,求a的取值范围.
考点:对数函数图象与性质的综合应用
专题:函数的性质及应用
分析:(1)根据对数函数的运算性质,将函数进行转化,利用二次函数根的取值建立不等式组,解不等式组即可得到结论.
(2)根据对数函数的性质,得到
>0恒成立,利用参数分离法即可求出a的取值范围.
(2)根据对数函数的性质,得到
| 1+2xa |
| 2 |
解答:
解:(1)∵f(x)=lg
(a∈R)
∴F(x)=2f(x)-f(2x)=2lg
-lg
,
由F(x)=0得2lg
=lg
,
即(
)2=
,
∴
=
,
即(a2-2a)22x+2a?2x-1=0,
设t=2x,则t>0,
则方程等价为(a2-2a)t2+2a?t-1=0,
∵函数F(x)=2f(x)-f(2x)有两个不同的零点,
∴(a2-2a)t2+2a?t-1=0有两个不同的正根,
则
,
即
,
∴
,即1<a<2,即a的取值范围是(1,2);
(2)若函数f(x)在定义域x∈(-∞,1]上有意义,
则当x≤1时,
>0恒成立,
即1+a•2x>0恒成立,
即a>
,
∵x≤1,
∴-
≤-
,
即a>-
,
∴a的取值范围是a>-
.
| 1+2xa |
| 2 |
∴F(x)=2f(x)-f(2x)=2lg
| 1+2xa |
| 2 |
| 1+22xa |
| 2 |
由F(x)=0得2lg
| 1+2xa |
| 2 |
| 1+22xa |
| 2 |
即(
| 1+2xa |
| 2 |
| 1+22xa |
| 2 |
∴
| 1+2a•2x+a2•22x |
| 4 |
| 1+22xa |
| 2 |
即(a2-2a)22x+2a?2x-1=0,
设t=2x,则t>0,
则方程等价为(a2-2a)t2+2a?t-1=0,
∵函数F(x)=2f(x)-f(2x)有两个不同的零点,
∴(a2-2a)t2+2a?t-1=0有两个不同的正根,
则
|
即
|
∴
|
(2)若函数f(x)在定义域x∈(-∞,1]上有意义,
则当x≤1时,
| 1+2xa |
| 2 |
即1+a•2x>0恒成立,
即a>
| -1 |
| 2x |
∵x≤1,
∴-
| 1 |
| 2x |
| 1 |
| 2 |
即a>-
| 1 |
| 2 |
∴a的取值范围是a>-
| 1 |
| 2 |
点评:本题主要考查对数的基本运算,以及对数函数的图象和性质,综合性较强,运算量较大,有一定的难度.

练习册系列答案
相关题目
已知三条直线a,b,c和平面β,则下列推论中正确的是( )
| A、若a∥b,b?β,则a∥β |
| B、若a∥β,b∥β,则a∥b或a与b相交 |
| C、若a⊥c,b⊥c,则a∥b |
| D、若a?β,b∥β,a,b共面,则a∥b |
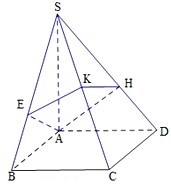 如图,四棱锥S-ABCD的底面是正方形,侧棱SA⊥底面ABCD,过A作AE垂直SB交SB于E点,作AH垂直SD交SD于H点,平面AEH交SC于K点,P是SA上的动点,且AB=1,SA=2.
如图,四棱锥S-ABCD的底面是正方形,侧棱SA⊥底面ABCD,过A作AE垂直SB交SB于E点,作AH垂直SD交SD于H点,平面AEH交SC于K点,P是SA上的动点,且AB=1,SA=2. 已知抛物线C:y=x2.过点M(1,2)的直线l交C于A,B两点.抛物线C在点A处的切线与在点B处的切线交于点P.
已知抛物线C:y=x2.过点M(1,2)的直线l交C于A,B两点.抛物线C在点A处的切线与在点B处的切线交于点P.