题目内容
已知m,n为异面直线,m⊥平面α,n⊥平面β,直线l满足l⊥m,l⊥n,lα,lβ,则( )
A.α∥β且l∥α
B.α⊥β且l⊥β
C.α与β相交,且交线垂直于l
D.α与β相交,且交线平行于l
D
[解析] 解法1:平移直线m使之与n相交于O,这两条直线确定的平面为γ,∵m⊥平面α,n⊥平面β,则平面α与平面β相交.设交线为a,则a⊥γ,又l⊥m,l⊥n,则l⊥γ,∴l∥a.
解法2:若α∥β,∵m⊥α,n⊥β,∴m∥n,这与m、n异面矛盾,故α与β相交,设α∩β=a,则a⊥m,a⊥n,在m上取点O,过O作n′∥n,设m与n′确定的平面为γ,∵a⊥m,a⊥n′,∴a⊥γ,∵l⊥n,∴l⊥n′,
又l⊥m,∴l⊥γ,∴a∥l.

练习册系列答案
 天天向上一本好卷系列答案
天天向上一本好卷系列答案 小学生10分钟应用题系列答案
小学生10分钟应用题系列答案
相关题目
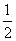 (AC+BD)(填“>”,“<”或“=”).
(AC+BD)(填“>”,“<”或“=”).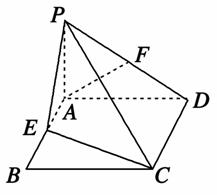
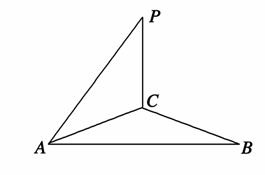
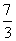 πa2
πa2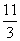 πa2 D.5πa2
πa2 D.5πa2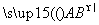 ,
,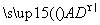 ,
,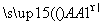 两两的夹角均为60°,且|
两两的夹角均为60°,且|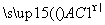 |=( )
|=( )