题目内容
设f(x)=x-alnx(a∈R),已知y=f(x)有两个零点x1,x2,且x1<x2.
(1)求a的取值范围;
(2)证明:x1+x2随着a的增大而增大.
(1)求a的取值范围;
(2)证明:x1+x2随着a的增大而增大.
考点:根的存在性及根的个数判断
专题:导数的综合应用
分析:(1)通过求导,得出切点坐标,找到函数y=f(x)有两个零点的等价条件,从而求出a的取值范围;
(2)令
=t(t>1),得到
,从而x1+x2=
,令m(x)=
,(x>1),通过求导得到函数的单调性,从而解决问题.
(2)令
| x2 |
| x1 |
|
| alnt(t+1) |
| t-1 |
| alnx(x+1) |
| x-1 |
解答:
解:(1)令f(x)=0,∴lnx=
x,
画出函数g(x)=lnx,h(x)=
x的图象,如图示:
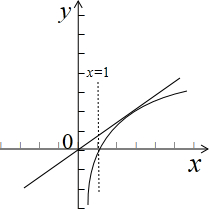 ,
,
∵g′(x)=
=
,∴切点坐标是(a,lna),
把(a,lna)代入h(x)=
x,得:a=e,
∴若y=f(x)有两个零点x1,x2,
即g(x),h(x)有2个交点,只需a>e即可;
∴a的范围是(e,+∞):
(2)∵x1=alnx1,x2=alnx2,∴x2-x1=aln
,
令
=t(t>1),
则:
,解得:x1=
,x2=
,
∴x1+x2=
,
令m(x)=
,(x>1),
则m′(x)=
,
∵a>e,x(x-1)2>0,
令n(x)=x2-2xlnx-1,
则n′(x)=2(x-lnx-1)>0,
∴n(x)在(1,+∞)递增,∴n(x)>n(1)=0,
∴m′(x)>0,m(x)在(1,+∞)递增,
∴x1+x2随着a的增大而增大.
| 1 |
| a |
画出函数g(x)=lnx,h(x)=
| 1 |
| a |
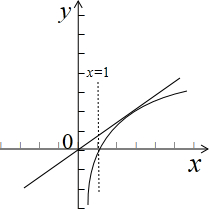 ,
,∵g′(x)=
| 1 |
| x |
| 1 |
| a |
把(a,lna)代入h(x)=
| 1 |
| a |
∴若y=f(x)有两个零点x1,x2,
即g(x),h(x)有2个交点,只需a>e即可;
∴a的范围是(e,+∞):
(2)∵x1=alnx1,x2=alnx2,∴x2-x1=aln
| x2 |
| x1 |
令
| x2 |
| x1 |
则:
|
| alnt |
| t-1 |
| atlnt |
| t-1 |
∴x1+x2=
| alnt(t+1) |
| t-1 |
令m(x)=
| alnx(x+1) |
| x-1 |
则m′(x)=
| a(x2-2xlnx-1) |
| x(x-1)2 |
∵a>e,x(x-1)2>0,
令n(x)=x2-2xlnx-1,
则n′(x)=2(x-lnx-1)>0,
∴n(x)在(1,+∞)递增,∴n(x)>n(1)=0,
∴m′(x)>0,m(x)在(1,+∞)递增,
∴x1+x2随着a的增大而增大.
点评:点评:本题考查了导数的运算以及利用导数研究函数的单调性与极值问题,也考查了函数思想、化归思想、抽象概括能力和分析问题、解决问题的能力,是综合型题目.

练习册系列答案
相关题目