题目内容
2.对任意实数a、b定义运算?:a?b=$\left\{\begin{array}{l}{b,a-b≥1}\\{a,a-b<1}\end{array}\right.$,设f(x)=(x2-1)?(4+x),若函数y=f(x)+k有三个零点,则实数k的取值范围是( )| A. | (-1,3] | B. | [-3,1] | C. | [-1,2) | D. | [-2,1) |
分析 利用新定义化简f(x)解析式,做出f(x)的函数图象,根据图象即可得出k的范围.
解答 解:解x2-1-(4+x)≥1得x≤-2或x≥3,
∴f(x)=$\left\{\begin{array}{l}{x+4,x≤-2或x≥3}\\{{x}^{2}-1,-2<x<3}\end{array}\right.$,
做出f(x)的函数图象,如图所示:
∵y=f(x)+k有三个零点,
∴-1<-k≤2,即-2≤k<1.
故选:D.
点评 本题考查了函数零点与函数图象的关系,不等式的解法,属于中档题.

练习册系列答案
相关题目
12.若△ABC的三边分别为a,b,c,且圆x2+y2=1与直线ax+by+c=0没有公共点,则△ABC一定是( )
| A. | 钝角三角形 | B. | 锐角三角形 | C. | 直角三角形 | D. | 不能确定 |
13.已知命题p:?x∈R,x2-2xsinθ+1≥0;命题q:?α,β∈R,sin(α+β)≤sinα+sinβ,则下列命题中的真命题为( )
| A. | (¬p)∧q | B. | ¬(p∧q) | C. | (¬p)∨q | D. | p∧(¬q) |
10.已知等比数列{an}的前n项和为Sn,若S2n=4(a1+a3+…+a2n-1),a1•a2•a3=27,则log3a1+log3a2+…+log3a20=( )
| A. | 210 | B. | 190 | C. | 220 | D. | 242 |
17.执行如图所示的程序框图,若x∈[a,b],y∈[0,4],则b-a的最小值为( )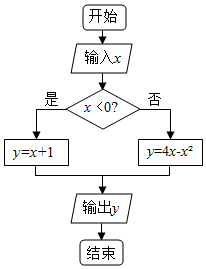

| A. | 2 | B. | 3 | C. | 4 | D. | 5 |
11.已知双曲线$\frac{x^2}{a^2}-\frac{y^2}{b^2}=1(a>b>0)$的左,右焦点分别为F1,F2,双曲线上一点P满足PF2⊥x轴,若|F1F2|=12,|PF2|=5,则该双曲线的离心率为( )
| A. | $\frac{13}{12}$ | B. | $\frac{12}{5}$ | C. | $\frac{3}{2}$ | D. | 3 |
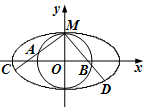 如图,圆O与离心率为$\frac{{\sqrt{3}}}{2}$的椭圆$\frac{x^2}{a^2}+\frac{y^2}{b^2}=1$(a>b>0)相切于点M(0,1).
如图,圆O与离心率为$\frac{{\sqrt{3}}}{2}$的椭圆$\frac{x^2}{a^2}+\frac{y^2}{b^2}=1$(a>b>0)相切于点M(0,1).