题目内容
7.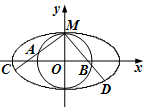 如图,圆O与离心率为$\frac{{\sqrt{3}}}{2}$的椭圆$\frac{x^2}{a^2}+\frac{y^2}{b^2}=1$(a>b>0)相切于点M(0,1).
如图,圆O与离心率为$\frac{{\sqrt{3}}}{2}$的椭圆$\frac{x^2}{a^2}+\frac{y^2}{b^2}=1$(a>b>0)相切于点M(0,1).(Ⅰ)求椭圆的方程;
(Ⅱ)过点M引两条互相垂直的两直线l1、l2与两曲线分别交于点A、C与点B、D(均不重合).
(ⅰ)若P为椭圆上任一点,记点P到两直线的距离分别为d1、d2,求$d_1^2+d_2^2$的最大值;
(ⅱ)若$3\overrightarrow{MA}•\overrightarrow{MC}=4\overrightarrow{MB}•\overrightarrow{MD}$,求l1与l2的方程.
分析 (Ⅰ)利用离心率以及椭圆的短轴端点,转化求解椭圆的方程即可.
(Ⅱ)(ⅰ)设P(x0,y0),通过l1⊥l2,结合$\frac{x_0^2}{4}+y_0^2=1$,推出-1≤y0≤1,利用二次函数求解$d_1^2+d_2^2$取得最大值,以及此时点P的坐标;
(ⅱ)设l1的方程为y=kx+1,由$\left\{\begin{array}{l}y=kx+1\\{x^2}+{y^2}=1\end{array}\right.$解得A,由$\left\{\begin{array}{l}y=kx+1\\ \frac{x^2}{4}+{y^2}=1\end{array}\right.$解得C,同理可得B,D,求出向量利用$3\overrightarrow{MA•}\overrightarrow{MC}=4\overrightarrow{MB}•\overrightarrow{MD}$求出直线的斜率k,端点直线方程即可.
解答 解:(Ⅰ)由题意:$\frac{c}{a}=\frac{{\sqrt{3}}}{2},b=1,{c^2}+{b^2}={a^2}$解得$a=2,b=1,c=\sqrt{3}$…(2分)
椭圆的方程为$\frac{x^2}{4}+{y^2}=1$…(3分)
(Ⅱ)(ⅰ)设P(x0,y0)因为l1⊥l2,则$d_1^2+d_2^2=P{M^2}=x_0^2+{({y_0}+1)^2}$因为$\frac{x_0^2}{4}+y_0^2=1$
所以$d_1^2+d_2^2=4-4y_0^2+{({y_0}+1)^2}=-3{({y_0}+\frac{1}{3})^2}+\frac{16}{3}$…(5分)
因为-1≤y0≤1
所以当${y_0}=-\frac{1}{3}$时$d_1^2+d_2^2$取得最大值为$\frac{16}{3}$,此时点$P(±\frac{{4\sqrt{2}}}{3},-\frac{1}{3})$…(6分)
(ⅱ)设l1的方程为y=kx+1,由$\left\{\begin{array}{l}y=kx+1\\{x^2}+{y^2}=1\end{array}\right.$解得$A(-\frac{2k}{{{k^2}+1}},\frac{{1-{k^2}}}{{1+{k^2}}})$
由$\left\{\begin{array}{l}y=kx+1\\ \frac{x^2}{4}+{y^2}=1\end{array}\right.$解得$C(-\frac{8k}{{4{k^2}+1}},\frac{{1-4{k^2}}}{{1+4{k^2}}})$…(8分)
同理可得$B(\frac{2k}{{{k^2}+1}},\frac{{{k^2}-1}}{{{k^2}+1}})$,$D(\frac{8k}{{{k^2}+4}},\frac{{{k^2}-4}}{{{k^2}+4}})$…(10分)
所以$\overrightarrow{MA}=(-\frac{2k}{{{k^2}+1}},\frac{{-2{k^2}}}{{1+{k^2}}})$,$\overrightarrow{MC}(-\frac{8k}{{4{k^2}+1}},\frac{{-8{k^2}}}{{1+4{k^2}}})$,$\overrightarrow{MB}=(\frac{2k}{{{k^2}+1}},\frac{-2}{{{k^2}+1}})$,$\overrightarrow{MD}=(\frac{8k}{{{k^2}+4}},\frac{-8}{{{k^2}+4}})$
由$3\overrightarrow{MA•}\overrightarrow{MC}=4\overrightarrow{MB}•\overrightarrow{MD}$得$\frac{{3{k^2}}}{{1+4{k^2}}}=\frac{4}{{{k^2}+4}}$解得$k=±\sqrt{2}$…(13分)
所以l1的方程为$y=\sqrt{2}x+1$,l2的方程为$y=-\frac{{\sqrt{2}}}{2}x+1$
或l1的方程为$y=-\sqrt{2}x+1$,l2的方程为$y=\frac{{\sqrt{2}}}{2}x+1$…(14分)
点评 本题考查直线与椭圆的位置关系的综合应用,向量的数量积的运算,椭圆方程的求法,考查转化思想以及计算能力.

| x | 2 | 5 | 8 | 9 | 11 |
| y | 12 | 10 | 8 | 8 | 7 |
(2)若天气预报明天的最低气温为10℃,用所求回归方程预测该店明天的营业额;
(3)设该地3月份的日最低气温X~N(μ,σ2),其中μ近似为样本平均数,σ2近似为样本方差,求P(0.6<X<3.8).
附:(1)回归方程$\stackrel{∧}{y}$=$\stackrel{∧}{b}$x+$\stackrel{∧}{a}$中,$\stackrel{∧}{b}$=$\frac{{{\sum_{i=1}^{n}x}_{i}y}_{i}-n\overline{x}\overline{y}}{{\sum_{i=1}^{n}x}_{i}^{2}-{n\overline{x}}^{2}}$,$\stackrel{∧}{a}$=$\overline{y}$-$\stackrel{∧}{b}$$\overline{x}$,22+52+82+92+112=295,2×12+5×10+8×8+9×8+11×7=287,
(2)$\sqrt{10}≈3.2$;若X~N(μ,σ2),则P(μ-σ<X<μ+σ)=0.6827,P(μ-2σ<X<μ+2σ)=0.9545.
| A. | $\frac{1}{4}$ | B. | $\frac{1}{2}$ | C. | $\frac{3}{4}$ | D. | $\frac{1}{3}$ |
| A. | (-1,3] | B. | [-3,1] | C. | [-1,2) | D. | [-2,1) |
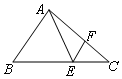 如图,在△ABC中,E,F分别是边BC,AC上的点,且△ABE是边长为3的正三角形,EF∥AB,EF=1,则sinC等于( )
如图,在△ABC中,E,F分别是边BC,AC上的点,且△ABE是边长为3的正三角形,EF∥AB,EF=1,则sinC等于( )| A. | $\frac{{\sqrt{7}}}{14}$ | B. | $\frac{{\sqrt{7}}}{7}$ | C. | $\frac{{\sqrt{21}}}{14}$ | D. | $\frac{{\sqrt{21}}}{7}$ |
| A. | ①② | B. | ②③ | C. | ①③ | D. | ①②③ |
| A. | $y=2\sqrt{2}x+1$ | B. | $y=\sqrt{3}x+1$ | C. | $y=\sqrt{2}x+1$ | D. | $y=2\sqrt{3}x+2$ |

 已知圆锥母线长为5,底面圆半径长为4,点M是母线PA的中点,AB是底面圆的直径,点C是弧AB的中点;
已知圆锥母线长为5,底面圆半径长为4,点M是母线PA的中点,AB是底面圆的直径,点C是弧AB的中点;