题目内容
17．执行如图所示的程序框图，若x∈[a，b]，y∈[0，4]，则b-a的最小值为（ ）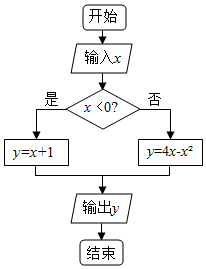
| A． | 2 | B． | 3 | C． | 4 | D． | 5 |
分析 写出分段函数，利用x∈[a，b]，y∈[0，4]，即可b-a的最小值．
解答 解：由题意，y=$\left\{\begin{array}{l}{x+1，x＜0}\\{4x-{x}^{2}，x≥0}\end{array}\right.$，
x∈[a，b]，y∈[0，4]，则b-a的最小值为2，此时区间为[0，2]或[2，4]，
故选A．
点评 本题考查程序框图，考查分段函数，考查学生分析解决问题的能力，属于中档题．
练习册系列答案
相关题目
2．对任意实数a、b定义运算?：a?b=$\left\{\begin{array}{l}{b，a-b≥1}\\{a，a-b＜1}\end{array}\right.$，设f（x）=（x2-1）?（4+x），若函数y=f（x）+k有三个零点，则实数k的取值范围是（ ）
| A． | （-1，3] | B． | [-3，1] | C． | [-1，2） | D． | [-2，1） |
9．设a、b、c是正实数，则“a、b、c依次成等差数列”是“$b≥\sqrt{ac}$”的（ ）
| A． | 充分而不必要条件 | B． | 必要而不充分条件 | ||
| C． | 充分必要条件 | D． | 既不充分也不必要条件 |
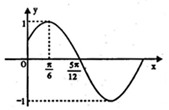已知函数f（x）=Msin（ωx+φ）（M＞0）的部分图象如图所示．
图形的对称，正弦曲线的流畅都能体现“数学美”．“黄金分割”也是数学美得 一种体现，如图，椭圆的中心在原点，F为左焦点，当$\overrightarrow{FB}⊥\overrightarrow{AB}$时，其离心率为$\frac{{\sqrt{5}-1}}{2}$，此类椭圆被称为“黄金椭圆”，类比“黄金椭圆”，可推算出“黄金双曲线”的离心率e等于$\frac{\sqrt{5}+1}{2}$．