题目内容
10.已知等比数列{an}的前n项和为Sn,若S2n=4(a1+a3+…+a2n-1),a1•a2•a3=27,则log3a1+log3a2+…+log3a20=( )| A. | 210 | B. | 190 | C. | 220 | D. | 242 |
分析 由等比数列的通项公式得a2=3,在S2n=4(a1+a3+…+a2n-1)中,由n=1,得a1=1,q=3,从而an=1×3n-1=3n-1,进而log3a1+log3a2+…+log3a20=$lo{g}_{3}({3}^{0}×3×{3}^{2}×…×{3}^{19})$,由此能求出结果.
解答 解:∵等比数列{an}的前n项和为Sn,
S2n=4(a1+a3+…+a2n-1),a1•a2•a3=27,
∴利用等比数列的性质可得,a1a2a3=a23=27 即a2=3,
∵S2n=4(a1+a3+…+a2n-1)
∴n=1时有,S2=a1+a2=4a1,解得a1=1,q=3,
∴an=1×3n-1=3n-1,
∴log3a1+log3a2+…+log3a20=log3(a1×a2×…×a20)
=$lo{g}_{3}({3}^{0}×3×{3}^{2}×…×{3}^{19})$=$lo{g}_{3}{3}^{190}$=190.
故选:B.
点评 本题考查了等差数列的通项公式,考查了等差数列的前n项和,是基础题.

练习册系列答案
相关题目
15.在区间[0,1]上随机选取两个数x和y,则y>2x的概率为( )
| A. | $\frac{1}{4}$ | B. | $\frac{1}{2}$ | C. | $\frac{3}{4}$ | D. | $\frac{1}{3}$ |
2.对任意实数a、b定义运算?:a?b=$\left\{\begin{array}{l}{b,a-b≥1}\\{a,a-b<1}\end{array}\right.$,设f(x)=(x2-1)?(4+x),若函数y=f(x)+k有三个零点,则实数k的取值范围是( )
| A. | (-1,3] | B. | [-3,1] | C. | [-1,2) | D. | [-2,1) |
20.执行如图所示的程序框图,则输出S的值为( )
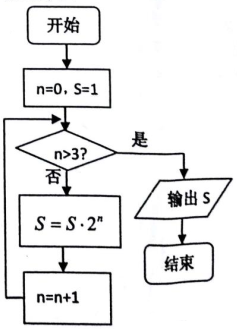

| A. | 16 | B. | 32 | C. | 64 | D. | 1024 |
 阅读右面的程序框图,当该程序运行后输出的x的值是13.
阅读右面的程序框图,当该程序运行后输出的x的值是13.
 已知圆锥母线长为5,底面圆半径长为4,点M是母线PA的中点,AB是底面圆的直径,点C是弧AB的中点;
已知圆锥母线长为5,底面圆半径长为4,点M是母线PA的中点,AB是底面圆的直径,点C是弧AB的中点;