题目内容
已知命题p:方程x2+mx+1=0有两个不相等的实根,命题q:不等式mx2-2(m+1)x+m+1<0对任意的实数x恒成立.若p∨q为假,求实数m的取值范围.
考点:复合命题的真假
专题:简易逻辑
分析:由已知推导出命题p:m>2或m<-2,命题q:m<-1.由p∨q为假,知p和q都是假命题,由此能求出实数m的取值范围.
解答:
解:∵方程x2+mx+1=0有两个不相等的实根,
∴△1=m2-4>0,解得m>2或m<-2,
∴命题p:m>2或m<-2,
∵不等式mx2-2(m+1)x+m+1<0对任意的实数x恒成立,
∴
,
解得m<-1,
∴命题q:m<-1.
∵p∨q为假,∴p和q都是假命题,
∴
,
∴-1≤m≤2.
∴实数m的取值范围是[-1,2].
∴△1=m2-4>0,解得m>2或m<-2,
∴命题p:m>2或m<-2,
∵不等式mx2-2(m+1)x+m+1<0对任意的实数x恒成立,
∴
|
解得m<-1,
∴命题q:m<-1.
∵p∨q为假,∴p和q都是假命题,
∴
|
∴-1≤m≤2.
∴实数m的取值范围是[-1,2].
点评:本题考查实数的取值范围的求法,是中档题,解题时要认真审题,注意不等式性质的合理运用.

练习册系列答案
 优秀生应用题卡口算天天练系列答案
优秀生应用题卡口算天天练系列答案 浙江之星课时优化作业系列答案
浙江之星课时优化作业系列答案 激活思维优加课堂系列答案
激活思维优加课堂系列答案
相关题目
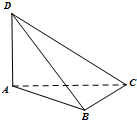 如图,在四面体ABCD中,已知DA⊥面ABC,BC⊥面ABD,BC=BD=2,四面体的三个面DAB、DBC、DCA面积的平方和是8,则∠ADB=
如图,在四面体ABCD中,已知DA⊥面ABC,BC⊥面ABD,BC=BD=2,四面体的三个面DAB、DBC、DCA面积的平方和是8,则∠ADB=