题目内容
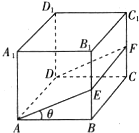 如图正方体ABCD-A1B1C1D1的棱长为1,点E在线段BB1和线段A1B1上移动,∠EAB=θ,θ∈(0,
如图正方体ABCD-A1B1C1D1的棱长为1,点E在线段BB1和线段A1B1上移动,∠EAB=θ,θ∈(0,| π |
| 2 |
| π |
| 2 |
A、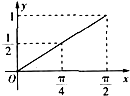 |
B、 |
C、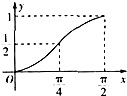 |
D、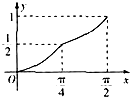 |
考点:函数的图象
专题:函数的性质及应用
分析:根据条件求出V=V(θ)的表达式,即可得到结论.
解答:
 解:当θ∈(0,
解:当θ∈(0,
]时,BE=tanθ,则三棱柱的体积为V(θ)=
tanθ,
当θ∈(
,
)时,AE=tan(
-θ)=cotθ,
则棱BC所在部分的体积为V(θ)=1-
tan(
-θ),
则函数V=V(θ),θ∈(0,
)的图象关于点(
,
)对称,
故选:C.
 解:当θ∈(0,
解:当θ∈(0,| π |
| 4 |
| 1 |
| 2 |
当θ∈(
| π |
| 4 |
| π |
| 2 |
| π |
| 2 |
则棱BC所在部分的体积为V(θ)=1-
| 1 |
| 2 |
| π |
| 2 |
则函数V=V(θ),θ∈(0,
| π |
| 2 |
| π |
| 4 |
| 1 |
| 2 |
故选:C.
点评:本题主要考查函数图象的识别和判断,利用条件求出体积的表达式是解决本题的关键.

练习册系列答案
 名师指导期末冲刺卷系列答案
名师指导期末冲刺卷系列答案
相关题目
已知函数f(x)=2x-2-x,则f(x)是( )
| A、奇函数且是增函数 |
| B、奇函数且是减函数 |
| C、偶函数且是增函数 |
| D、偶函数且是减函数 |
已知sinα-sinβ=
,cosα-cosβ=
,则cos2
等于( )
| ||
| 3 |
| ||
| 3 |
| α-β |
| 2 |
A、
| ||
B、
| ||
C、
| ||
D、
|
已知集合A={x|x2<4x},集合B={y|y=-x2,-1≤x≤2},则集合∁R(A∩B)=( )
| A、R | B、{0} |
| C、∅ | D、{x|x≥4或x≤0} |
直线3x+4y=5与圆(x-1)2+(y+2)2=5的位置关系是( )
| A、外离 | B、外切 | C、相交 | D、内切 |
下列命题中,真命题的是( )
| A、?0∈R,e x0≤0 |
| B、?x∈R,2x>x2 |
| C、a-b>0是a3-b3>0的充分不必要条件 |
| D、ab>1是a>1且b>1的必要不充分条件 |
已知双曲线
-
=1(a>0,b>0)的右焦点为F(c,0),直线x=
与一条渐近线交于点A,△OAF的面积为
(O为原点),则抛物线y2=
x的准线方程为( )
| x2 |
| a2 |
| y2 |
| b2 |
| a2 |
| c |
| a2 |
| 2 |
| 4a |
| b |
| A、x=-1 | B、x=-2 |
| C、y=-1 | D、y=-2 |