题目内容
已知x2=y2+18，求证：x，y不都是整数．
考点：反证法与放缩法
专题：推理和证明
分析：假设x，y都是整数，利用已知条件，推出等式不成立，说明假设错误目得到结果．
解答：
证明：假设x，y都是整数
x2=y2+18，
即x2-y2=18，
（x-y）（x+y）=18=2×3×3，
x，y都是整数
∴x-y，x+y都是整数，而且x-y，x+y有相同的奇偶性，等式的右侧2×3×3，
所以等式不成立，
假设错误．
∴x，y不都是整数．
x2=y2+18，
即x2-y2=18，
（x-y）（x+y）=18=2×3×3，
x，y都是整数
∴x-y，x+y都是整数，而且x-y，x+y有相同的奇偶性，等式的右侧2×3×3，
所以等式不成立，
假设错误．
∴x，y不都是整数．
点评：本题考查反证法证明问题的方法，推出矛盾结果是解题的关键．
练习册系列答案
相关题目
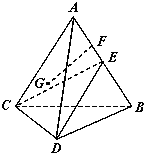如图，在四面体ABCD中，BC=AC，AD=BD，E是AB的中点．
如图，AB是圆O的直径，点C是圆O上异于A、B的点，直线PC⊥平面ABC，E，F分别为PA，PC的中点．
如图，在正方体ABCD-A1B1C1D1中，E为AB的中点．