题目内容
设z=
+
i(i是虚数单位),则z+2z2+3z3+4z4+5z5+6z6= .
| 1 |
| 2 |
| ||
| 2 |
考点:复数代数形式的混合运算
专题:数系的扩充和复数
分析:把复数的代数形式转化成三角形式,进行复数的乘方的运算,再化成代数形式即可.
解答:
解:∵z=
+
i=cos
+isin
,
∴z+2z2+3z3+4z4+5z5+6z6=cos
+isin
+2cos
+2isin
+3cosπ+3isinπ+
4cos
+4isin
+5cos
+5isin
+6cos2π+6isin2π
=6(
-
i)=3-3
i,
故答案为:3-3
i
| 1 |
| 2 |
| ||
| 2 |
| π |
| 3 |
| π |
| 3 |
∴z+2z2+3z3+4z4+5z5+6z6=cos
| π |
| 3 |
| π |
| 3 |
+2cos
| 2π |
| 3 |
| 2π |
| 3 |
4cos
| 4π |
| 3 |
| 4π |
| 3 |
| 5π |
| 3 |
| 5π |
| 3 |
+6cos2π+6isin2π
=6(
| 1 |
| 2 |
| ||
| 2 |
| 3 |
故答案为:3-3
| 3 |
点评:本题考查复数的代数形式的混合运算,化为三角形式是解决问题的关键,属基础题.

练习册系列答案
 云南师大附小一线名师提优作业系列答案
云南师大附小一线名师提优作业系列答案 冲刺100分单元优化练考卷系列答案
冲刺100分单元优化练考卷系列答案
相关题目
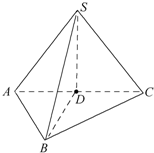 已知直角△ABC所在平面外一点S,且SA=SB=SC,D为斜边AC中点.
已知直角△ABC所在平面外一点S,且SA=SB=SC,D为斜边AC中点.