题目内容
 如图,AB是圆O的直径,点C是圆O上异于A、B的点,直线PC⊥平面ABC,E,F分别为PA,PC的中点.
如图,AB是圆O的直径,点C是圆O上异于A、B的点,直线PC⊥平面ABC,E,F分别为PA,PC的中点.(Ⅰ)记平面BEF与平面ABC的交线为l,试判断l与平面PAC的位置关系,并加以说明;
(Ⅱ)设(Ⅰ)中的直线l与圆O的另一个交点为D,且点Q满足
| DQ |
| 1 |
| 2 |
| CP |
①求证:sinθ=sinα•sinβ.
②当点C为弧AB的中点时,PC=AB,求直线DQ与平面BEF所成的角的正弦值.
考点:点、线、面间的距离计算,直线与平面所成的角,与二面角有关的立体几何综合题
专题:综合题,空间位置关系与距离,空间角
分析:(I)由已知条件推导出EF∥AC,从而得到EF∥平面ABC,由此能证明l∥平面PAC.
(II)①过B作AC的平行线BD,交线l即为直线BD,且l∥AC,由已知条件推导出∠CBF=β,∠CDF=θ,∠BDF=α,由此能证明sinθ=sinαsinβ;
②因为DQ∥CP,所以直线DQ与平面BEF所成的角就为CF与平面BEF所成的角,过点C作CG⊥BF,垂足为G,证明∠CFB就是直线CF与平面BEF所成的角,即可得出结论.
(II)①过B作AC的平行线BD,交线l即为直线BD,且l∥AC,由已知条件推导出∠CBF=β,∠CDF=θ,∠BDF=α,由此能证明sinθ=sinαsinβ;
②因为DQ∥CP,所以直线DQ与平面BEF所成的角就为CF与平面BEF所成的角,过点C作CG⊥BF,垂足为G,证明∠CFB就是直线CF与平面BEF所成的角,即可得出结论.
解答:
 解:(Ⅰ)直线l∥平面PAC,
解:(Ⅰ)直线l∥平面PAC,
证明如下:连接EF,
因为E,F分别是PA,PC的中点,所以EF∥AC.
又EF?平面ABC,且AC?平面ABC,所以EF∥平面ABC.
而EF?平面BEF,且平面BEF∩平面ABC=l,所以EF∥l.
因为l?平面PAC,EF?平面PAC,所以直线l∥平面PAC..4分
(Ⅱ)①证明:如图,连接BD,由(Ⅰ)可知交线l即为直线BD,且l∥AC.
因为AB是⊙O的直径,所以AC⊥BC,于是l⊥BC.
已知PC⊥平面ABC,而l?平面ABC,所以PC⊥l.
而PC∩BC=C,所以l⊥平面PBC.
连接BE,BF,
因为BF?平面PBC,所以l⊥BF.
故∠CBF就是二面角E-l-C的平面角,即∠CBF=β.
由
=
,作DQ∥CP,且DQ=
CP.
连接PQ,DF,
因为F是CP的中点,CP=2PF,所以DQ=PF,
从而四边形DQPF是平行四边形,PQ∥FD.
连接CD,因为PC⊥平面ABC,所以CD是FD在平面ABC内的射影,
故∠CDF就是直线PQ与平面ABC所成的角,即∠CDF=θ.
又BD⊥平面PBC,有BD⊥BF,知∠BDF为锐角,
故∠BDF为异面直线PQ与EF所成的角,即∠BDF=α,8 分
于是在Rt△DCF,Rt△FBD,Rt△BCF中,分别可得sinθ=
,sinα=
,sinβ=
,
从而sinαsinβ=
•
=
=sinθ,即sinθ=sinαsinβ.9分
②解:因为DQ∥CP,所以直线DQ与平面BEF所成的角就为CF与平面BEF所成的角
过点C作CG⊥BF,垂足为G,
因为BD⊥平面PBC,所以BD⊥CG,
又BD∩BF=B,所以CG⊥平面BEF
故∠CFB就是直线CF与平面BEF所成的角,sin∠CFB=
,
故直线DQ与平面BEF所成的角的正弦值为
13分
 解:(Ⅰ)直线l∥平面PAC,
解:(Ⅰ)直线l∥平面PAC,证明如下:连接EF,
因为E,F分别是PA,PC的中点,所以EF∥AC.
又EF?平面ABC,且AC?平面ABC,所以EF∥平面ABC.
而EF?平面BEF,且平面BEF∩平面ABC=l,所以EF∥l.
因为l?平面PAC,EF?平面PAC,所以直线l∥平面PAC..4分
(Ⅱ)①证明:如图,连接BD,由(Ⅰ)可知交线l即为直线BD,且l∥AC.
因为AB是⊙O的直径,所以AC⊥BC,于是l⊥BC.
已知PC⊥平面ABC,而l?平面ABC,所以PC⊥l.
而PC∩BC=C,所以l⊥平面PBC.
连接BE,BF,
因为BF?平面PBC,所以l⊥BF.
故∠CBF就是二面角E-l-C的平面角,即∠CBF=β.
由
| DQ |
| 1 |
| 2 |
| CP |
| 1 |
| 2 |
连接PQ,DF,
因为F是CP的中点,CP=2PF,所以DQ=PF,
从而四边形DQPF是平行四边形,PQ∥FD.
连接CD,因为PC⊥平面ABC,所以CD是FD在平面ABC内的射影,
故∠CDF就是直线PQ与平面ABC所成的角,即∠CDF=θ.
又BD⊥平面PBC,有BD⊥BF,知∠BDF为锐角,
故∠BDF为异面直线PQ与EF所成的角,即∠BDF=α,8 分
于是在Rt△DCF,Rt△FBD,Rt△BCF中,分别可得sinθ=
| CF |
| DF |
| BF |
| DF |
| CF |
| BF |
从而sinαsinβ=
| CF |
| BF |
| BF |
| DF |
| CF |
| DF |
②解:因为DQ∥CP,所以直线DQ与平面BEF所成的角就为CF与平面BEF所成的角
过点C作CG⊥BF,垂足为G,
因为BD⊥平面PBC,所以BD⊥CG,
又BD∩BF=B,所以CG⊥平面BEF
故∠CFB就是直线CF与平面BEF所成的角,sin∠CFB=
| ||
| 3 |
故直线DQ与平面BEF所成的角的正弦值为
| ||
| 3 |
点评:本题考查直线与平面的位置关系的判断与证明,考查三角函数正弦值相等的证明,解题时要认真审题,注意空间思维能力的培养.

练习册系列答案
 阅读快车系列答案
阅读快车系列答案
相关题目
 如图,在直四棱柱ABCD-A1B1C1D1中,底面ABCD为直角梯形,AB∥CD且∠ADC=90°,AD=1,CD=
如图,在直四棱柱ABCD-A1B1C1D1中,底面ABCD为直角梯形,AB∥CD且∠ADC=90°,AD=1,CD=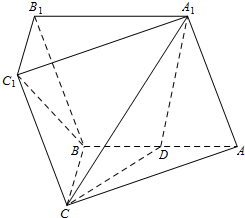 如图,在三棱柱ABC-A1B1C1中,侧面AA1B1B为菱形,且∠A1AB=60°,AC=BC,D是AB的中点.
如图,在三棱柱ABC-A1B1C1中,侧面AA1B1B为菱形,且∠A1AB=60°,AC=BC,D是AB的中点. 如图所示,P是△ABC内一点,且满足
如图所示,P是△ABC内一点,且满足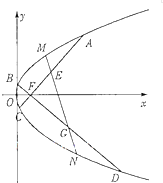 如图,已知点F为抛物线C1:y2=4x的焦点,过点F任作两条互相垂直的直线l1,l2,分别交抛物线C1于A,C,B,D四点,E,G分别为AC,BD的中点.
如图,已知点F为抛物线C1:y2=4x的焦点,过点F任作两条互相垂直的直线l1,l2,分别交抛物线C1于A,C,B,D四点,E,G分别为AC,BD的中点. 如图,设α∈(0,π),且α≠
如图,设α∈(0,π),且α≠