题目内容
（立体几何）正三棱锥D-ABC的底面边长为4，侧棱的长为8，过A点做与侧棱DB、DC分别交于E、F，那么△AEF周长的最小值是 ．
考点：多面体和旋转体表面上的最短距离问题
专题：空间位置关系与距离
分析：根据给出的正三棱锥的侧棱长和底面边长知，两条侧棱的夹角为锐角，然后求出该锐角的三倍角的余弦值，使原图形中的△AEF的周长最小，就是求沿PA剪开再展开后A点与A′点的最短距离，即直线距离，运用余弦定理可求解．
解答：
解：沿三棱锥P-ABC的侧棱PA剪开后再展开，如图，
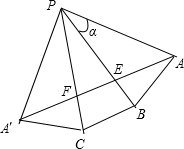
原图中△AEF的周长最小，也就是展开图中的AA′，
在△PAB中，因为PA=PB=8，AB=4，
设∠APB=α，则cosα=
=
=
．
∠APA′=3α，
由cos3α=4cos3α-3cosα=4×（
）3-3×
=
．
在△APA′中，由余弦定理得：
AA′2=PA2+PA′2-2PA•PA′cos3α
=82+82-2×8×8×
=121．
所以，AA′=11．
所以，△AEF的周长最小值为11．
故答案为：11
原图中△AEF的周长最小，也就是展开图中的AA′，
在△PAB中，因为PA=PB=8，AB=4，
设∠APB=α，则cosα=
| PA2+PB2-AB2 |
| 2PA•PB |
| 82+82-42 |
| 2×8×8 |
| 7 |
| 8 |
∠APA′=3α，
由cos3α=4cos3α-3cosα=4×（
| 7 |
| 8 |
| 7 |
| 8 |
| 7 |
| 128 |
在△APA′中，由余弦定理得：
AA′2=PA2+PA′2-2PA•PA′cos3α
=82+82-2×8×8×
| 7 |
| 128 |
所以，AA′=11．
所以，△AEF的周长最小值为11．
故答案为：11
点评：本题考查了棱锥的结构特征，考查了距离最短问题，该类问题通常比喻“蚂蚁爬行问题”，解答的方法是沿一定的棱或母线把多面体或旋转体剪开，然后再展开，求两点间的直线距离问题，是中档题．
练习册系列答案
阅读快车系列答案
相关题目
如图，设α∈（0，π），且α≠下面对相关系数r描述正确的是（ ）
| A、r＞0表两个变量负相关 |
| B、r＞1表两个变量正相关 |
| C、r 只能大于零 |
| D、|r|越接近于零，两个变量相关关系越弱 |