设i为虚数单位.则$\frac{2+i}{1-i}$-(1-i)=$-\frac{1}{2}+\frac{5}{2}i$．题目和参考答案——青夏教育精英家教网——

题目内容

10．设i为虚数单位，则$\frac{2+i}{1-i}$-（1-i）=$-\frac{1}{2}+\frac{5}{2}i$．

分析直接利用复数代数形式的乘除运算化简得答案．

解答解：$\frac{2+i}{1-i}$-（1-i）=$\frac{（2+i）（1+i）}{（1-i）（1+i）}-1+i=\frac{1+3i}{2}-1+i=-\frac{1}{2}+\frac{5}{2}i$，
故答案为：$-\frac{1}{2}+\frac{5}{2}i$．

点评本题考查复数代数形式的乘除运算，是基础的计算题．

练习册系列答案

1加1阅读好卷系列答案

专项复习训练系列答案

初中语文教与学阅读系列答案

阅读快车系列答案

完形填空与阅读理解周秘计划系列答案

英语阅读理解150篇系列答案

奔腾英语系列答案

标准阅读系列答案

53English系列答案

考纲强化阅读系列答案

相关题目

20．某几何体的三视图如图所示，则其表面积为（　　）

1．已知复数z₁=2t+i，z₂=1-2i，若$\frac{z_1}{z_2}$为实数，则实数t的值是（　　）

18．已知集合A={0，1，2，3，4}，B={m|m=2n，n∈A}，M={x∈R|x＞2}，则集合B∩∁_RM={0，2}．

5．已知数列{a_n}满足a_n+2-a_n=d（d∈R，且d≠0），n∈N*，a₁=2，a₂=2，且a₁，a₃，a₇成等比数列．
（Ⅰ）求d的值及数列{a_n}的通项公式；
（Ⅱ）设b_n=$\frac{（n+1）^{2}}{{a}_{n}•{a}_{n+1}}$，c_n=（-1）ⁿ•b_n，求数列{c_n}的前2n项和S_2n．

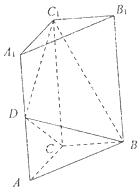如图，直三棱柱ABC-A₁B₁C₁中，AC⊥BC，AC=BC=$\frac{1}{2}$AA₁=1，D是棱AA₁上的点，DC₁⊥BD
（Ⅰ）求证：D为AA₁中点；
（Ⅱ）求直线BC₁与平面BDC所成角正弦值大小；
（Ⅲ）在△ABC边界及内部是否存在点M，使得B₁M⊥面BDC，存在，说明M位置，不存在，说明理由．

5．在平面直角坐标系xOy中，已知直线l的参数方程为$\left\{\begin{array}{l}x=1-\frac{1}{2}t\\ y=\frac{{\sqrt{3}}}{2}t\end{array}\right.$（t为参数），以原点O为极点，以x轴的正半轴为极轴建立极坐标系，曲线C的极坐标方程为ρ=6cosθ．
（Ⅰ）写出直线l的普通方程和曲线C的直角坐标方程；
（Ⅱ）若点P的直角坐标为（1，0），曲线C与直线l交于A，B两点，求|PA|+|PB|的值．

2．设全集U=R，集合A={x|x²-x-2＞0}，B={x|x²-3x-10＜0}，求∁_UA，∁_UB，A∩B，∁_UA∪B．

3．已知全集U=Z，A={x|x²-x-2＜0，x∈Z}，B={-1，0，1，2}，则（∁_UA）∩B等于（　　）