题目内容
1.已知复数z1=2t+i,z2=1-2i,若$\frac{z_1}{z_2}$为实数,则实数t的值是( )| A. | 1 | B. | -1 | C. | $\frac{1}{4}$ | D. | -$\frac{1}{4}$ |
分析 把z1=2t+i,z2=1-2i代入$\frac{z_1}{z_2}$,利用复数代数形式的乘除运算化简,再由虚部为0得答案.
解答 解:∵z1=2t+i,z2=1-2i,
∴$\frac{z_1}{z_2}$=$\frac{2t+i}{1-2i}=\frac{(2t+i)(1+2i)}{(1-2i)(1+2i)}=\frac{(2t-2)+(4t+1)i}{5}$,
又$\frac{z_1}{z_2}$为实数,∴4t+1=0,即t=$-\frac{1}{4}$.
故选:D.
点评 本题考查复数代数形式的乘除运算,考查复数的基本概念,是基础的计算题.

练习册系列答案
相关题目
12.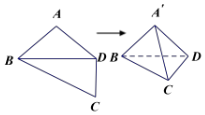 如图,在平面四边形ABCD中,AB=AD=CD=1,$BD=\sqrt{2}$,BD⊥CD,将其沿对角线BD折成四面体A′-BCD,使平面A′BD⊥平面BCD,若四面体A′-BCD顶点在同一球面上,则该球的表面积为( )
如图,在平面四边形ABCD中,AB=AD=CD=1,$BD=\sqrt{2}$,BD⊥CD,将其沿对角线BD折成四面体A′-BCD,使平面A′BD⊥平面BCD,若四面体A′-BCD顶点在同一球面上,则该球的表面积为( )
 如图,在平面四边形ABCD中,AB=AD=CD=1,$BD=\sqrt{2}$,BD⊥CD,将其沿对角线BD折成四面体A′-BCD,使平面A′BD⊥平面BCD,若四面体A′-BCD顶点在同一球面上,则该球的表面积为( )
如图,在平面四边形ABCD中,AB=AD=CD=1,$BD=\sqrt{2}$,BD⊥CD,将其沿对角线BD折成四面体A′-BCD,使平面A′BD⊥平面BCD,若四面体A′-BCD顶点在同一球面上,则该球的表面积为( )| A. | $\frac{{\sqrt{3}}}{2}π$ | B. | 3π | C. | $\frac{{\sqrt{2}}}{3}π$ | D. | 2π |
9.将函数y=$\sqrt{3}$cosx+sinx(x∈R)的图象向左平移m(m>0)个单位长度后,所得到的图象关于y轴对称,则m的最小值是( )
| A. | $\frac{π}{3}$ | B. | $\frac{π}{12}$ | C. | $\frac{π}{6}$ | D. | $\frac{5π}{6}$ |
13.i为虚数单位,复数(1+i)2+$\frac{2}{1-i}$的共轭复数是( )
| A. | 1+3i | B. | -1+3i | C. | 1-3i | D. | -1-3i |
14.i为虚数单位,复数$\frac{1+3i}{1-i}$=( )
| A. | -1+2i | B. | 1-2i | C. | -1-2i | D. | 1+2i |
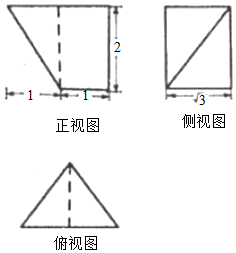
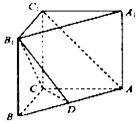 如图,直三棱柱ABC-A1B1C1中,AC=4,BC=3,AA1=4,AC⊥BC,点D在线段AB上.
如图,直三棱柱ABC-A1B1C1中,AC=4,BC=3,AA1=4,AC⊥BC,点D在线段AB上.