题目内容
15.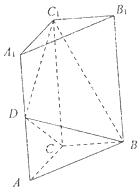 如图,直三棱柱ABC-A1B1C1中,AC⊥BC,AC=BC=$\frac{1}{2}$AA1=1,D是棱AA1上的点,DC1⊥BD
如图,直三棱柱ABC-A1B1C1中,AC⊥BC,AC=BC=$\frac{1}{2}$AA1=1,D是棱AA1上的点,DC1⊥BD(Ⅰ)求证:D为AA1中点;
(Ⅱ)求直线BC1与平面BDC所成角正弦值大小;
(Ⅲ)在△ABC边界及内部是否存在点M,使得B1M⊥面BDC,存在,说明M位置,不存在,说明理由.
分析 (Ⅰ)根据题意以CA、CB、CC1所在直线为x,y,z轴,建立空间直角坐标系,利用向量法能证明D为AA1的中点.
(Ⅱ)求出面BDC的法向量,利用向量法能求出直线BC1与平面BDC所成角正弦值.
(Ⅲ)设M(x,y,0),0≤x≤1,0≤y≤1,x+y≤1,利用向量法推导出在△ABC边界及内部是不存在点M,使得B1M⊥面BDC.
解答 证明:(Ⅰ)根据题意以CA、CB、CC1所在直线为x,y,z轴,
建立空间直角坐标系,
∴D(1,0,h),C1(0,0,2),B(0,1,0),B1(0,1,2),
∴$\overrightarrow{D{C}_{1}}$=(-1,0,2-h),$\overrightarrow{BD}$=(1,-1,h),
∴-1+h(2-h)=0,解得h=1,
∴D为AA1的中点.
(Ⅱ)$\overrightarrow{B{C}_{1}}$=(0,-1,2),
设面BDC的法向量$\overrightarrow{n}$=(x,y,z),
则$\left\{\begin{array}{l}{\overrightarrow{n}•\overrightarrow{CB}=x+z=0}\\{\overrightarrow{n}•\overrightarrow{CD}=y=0}\end{array}\right.$,设x=1,得$\overrightarrow{n}$=(1,0,-1),
设直线BC1与平面BDC所成角为θ,
则sinθ=$\frac{|\overrightarrow{B{C}_{1}}•\overrightarrow{n}|}{|\overrightarrow{B{C}_{1}}|•|\overrightarrow{n}|}$=$\frac{2}{\sqrt{5}•\sqrt{2}}$=$\frac{\sqrt{10}}{5}$.
∴直线BC1与平面BDC所成角正弦值大小为$\frac{\sqrt{10}}{5}$.
(Ⅲ)设M(x,y,0),0≤x≤1,0≤y≤1,x+y≤1,
∴$\overrightarrow{{B}_{1}M}=(x,y-1,-2)$,
∵B1M⊥面BDC,∴$\overrightarrow{{B}_{1}M}=λ(1,0,-1)$,
∴$\left\{\begin{array}{l}{x=λ}\\{y-1=0}\\{-λ=-2}\end{array}\right.$,解得$\left\{\begin{array}{l}{x=2}\\{y=1}\end{array}\right.$,
∵x>1,∴在△ABC边界及内部是不存在点M,使得B1M⊥面BDC.
点评 本题考查点为线段中点的证明、线面角正弦值求法、满足线面垂直的点是否存在的判断等基础知识,考查推理论证能力、运算求解能力、空间想象能力、数据处理能力,考查函数与方程思想、化归与转化思想、数形结合,考查创新意识、应用意识,是中档题.

 全优点练单元计划系列答案
全优点练单元计划系列答案
| A. | $\frac{64}{3}$ | B. | 32 | C. | 64 | D. | $\frac{32}{3}$ |
| A. | a≤-2或a=1 | B. | a≤2或1≤a≤2 | C. | a≥1 | D. | -2≤a≤1 |
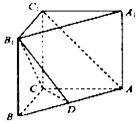 如图,直三棱柱ABC-A1B1C1中,AC=4,BC=3,AA1=4,AC⊥BC,点D在线段AB上.
如图,直三棱柱ABC-A1B1C1中,AC=4,BC=3,AA1=4,AC⊥BC,点D在线段AB上.