题目内容
5.已知数列{an}满足an+2-an=d(d∈R,且d≠0),n∈N*,a1=2,a2=2,且a1,a3,a7成等比数列.(Ⅰ)求d的值及数列{an}的通项公式;
(Ⅱ)设bn=$\frac{(n+1)^{2}}{{a}_{n}•{a}_{n+1}}$,cn=(-1)n•bn,求数列{cn}的前2n项和S2n.
分析 (Ⅰ)由已知求得a3=2+d,a7=2+3d,结合a1,a3,a7成等比数列求得d,可得an+2-an=2.然后分n为偶数和n为奇数求出数列{an}的通项公式;
(Ⅱ)把an代入bn=$\frac{(n+1)^{2}}{{a}_{n}•{a}_{n+1}}$,再求出${b}_{2n-1}=\frac{(2n)^{2}}{2n•2n}=1$.结合cn=(-1)n•bn,可得${c}_{2n-1}+{c}_{2n}=(-1)^{2n-1}{b}_{2n-1}+(-1)^{2n}{b}_{2n}$=$\frac{1}{4}(\frac{1}{n}-\frac{1}{n+1})$.则数列{cn}的前2n项和S2n可求.
解答 解:(Ⅰ)由已知,a3=2+d,a7=2+3d,
∵a1,a3,a7成等比数列,
∴(2+d)2=2(2+3d),解得d=2或d=0(舍).
于是an+2-an=2.
当n=2k时,an=a2k=a2+(k-1)×2=2k=n;
当n=2k-1时,an=a2k-1=a1+(k-1)×2=2k=n+1.
∴${a}_{n}=\left\{\begin{array}{l}{n,n为偶数}\\{n+1,n为奇数}\end{array}\right.$;
(Ⅱ)bn=$\frac{(n+1)^{2}}{{a}_{n}•{a}_{n+1}}$=$\frac{4{n}^{2}+4n+1}{4n(n+1)}=1+\frac{1}{4}(\frac{1}{n}-\frac{1}{n+1})$,
${b}_{2n-1}=\frac{(2n)^{2}}{2n•2n}=1$.
又cn=(-1)n•bn,
∴${c}_{2n-1}+{c}_{2n}=(-1)^{2n-1}{b}_{2n-1}+(-1)^{2n}{b}_{2n}$=$\frac{1}{4}(\frac{1}{n}-\frac{1}{n+1})$.
于是,${S}_{2n}=\frac{1}{4}(1-\frac{1}{2}+\frac{1}{2}-\frac{1}{3}+…+\frac{1}{n}-\frac{1}{n+1})=\frac{n}{4(n+1)}$.
点评 本题考查数列递推式,考查了等差数列和等比数列的性质,训练了裂项相消法求数列的前n项和,是中档题.

 百年学典课时学练测系列答案
百年学典课时学练测系列答案| A. | 1+3i | B. | -1+3i | C. | 1-3i | D. | -1-3i |
| A. | 若l∥α,α⊥β,则l⊥β | B. | 若l∥α,α∥β,则l∥β | C. | 若l⊥α,α∥β,则l⊥β | D. | 若l⊥α,α⊥β,则l∥β |
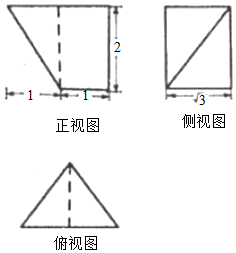

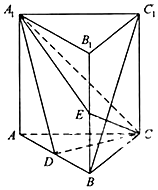 如图,直三棱柱ABC-A1B1C1中,D,E分别是AB,BB1的中点,AA1=AC=CB=$\frac{{\sqrt{2}}}{2}$AB.
如图,直三棱柱ABC-A1B1C1中,D,E分别是AB,BB1的中点,AA1=AC=CB=$\frac{{\sqrt{2}}}{2}$AB.