Question

已知一个正三棱台的两底面边长分别为30cm和20cm，且其侧面积等于两底面积之和，求棱台的高．

Answer 1

考点：棱台的结构特征

专题：空间位置关系与距离

分析：利用棱台的高、斜高、边心距构成直角梯形，通过构造直角三角形，利用勾股定理求出棱台的高．

解答： 解：如图所示，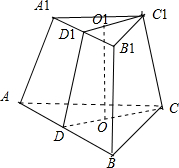
在正三棱台ABC-A₁B₁C₁中，
两底面边长分别为AB=30cm，A₁B₁=20cm，
∴侧面积为S_侧=3×

1

2

×（30+20）•DD₁，
两底面积之和为S_底=

3

4

×（30²+20²），
∵S_侧=S_底，
∴

3×50

2

•DD₁=

3

4

×1300，
解得DD₁=

13 3

3

，
∴OO12=(

13 3

3

)2-(

3

2

×30×

1

3

-

3

2

×20×

1

3

)2=

144

3

，
∴OO₁=

12 3

3

=4

3

；
即棱台的高为4

3

．

点评：本题考查了求正三棱台的高的问题，解题时应画出图形，结合图形解答问题，是计算题目．