题目内容

设不等式组
x+y≤π
x-y≥0
y≥0
所表示的区域为M，函数y=sinx，x∈[0，π]的图象与x轴所围成的区域为N，向M内随机投一个点，则该点落在N内的概率为
 
．
考点：几何概型,二元一次不等式（组）与平面区域
专题：概率与统计
分析：作出不等式组对应的平面区域，利用积分的应用求出区域N的面积，根据几何概型的概率公式，即可得到结论．
解答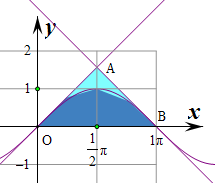： 解：作出不等式组对应的平面区域如图：为△AOB，
则B（π，0），由
x+y=π
x-y=0
得
x=
π
2
y=
π
2
，
即A（
π
2
，
π
2
），
则△AOB的面积S=
1
2
×π×
π
2
=
π2
4
，
由积分的几何意义可知区域N的面积为
∫
π
0
sinxdx=-cosx
|
π
0
=2，
根据几何概型的概率公式可知所求的概率P=
2
π2
4
=
8
π2
，
故答案为：
8
π2
点评：本题主要考查几何概型的概率计算，利用不等式组表示平面区域以及利用积分的几何意义求出相应的面积是解决本题的关键．
练习册系列答案
相关题目
欧阳修《卖油翁》中写到：（翁）乃取一葫芦置于地，以钱覆其口，徐以杓酌油沥之，自钱孔入，而钱不湿．己知铜钱是直径为4cm的圆面，中间有边长为1cm的正方形孔，若随机向铜钱上滴一滴油（油滴整体落在铜钱内），则油滴整体（油滴是直径为0.2cm的球）正好落入孔中的概率是
 
（不作近似计算）．
已知函数f（x）=ex（x2-x+1）-m，若?a，b，c∈R，且a＜b＜c，使得f（a）=f（b）=f（c）=0．则实数m的取值范围是（　　）
A、（-∞，1）
B、（1，
3
e
）
C、（1，e3）
D、（-∞，1）∪（e3，+∞）
袋中装有黑球和白球共7个，从中任取2个球都是黑球的概率为
2
7
，现有甲、乙两人从袋中轮流摸取1球，甲先取，乙后取，然后甲再取…，取球后不放回，直到两人中有一人取到白球时终止，每个球在每一次被取出的机会是等可能的，用ξ表示取球终止所需要的取球次数．
（Ⅰ）求随机变量ξ的分布列及数学期望；
（Ⅱ）求乙取到白球的概率．
已知椭圆的中心在原点，焦点在x轴上，左焦点到坐标原点、右焦点、右准线的距离依次成等差数列．
（1）求椭圆的离心率
（2）若直线l与此椭圆相交于A，B两点，且AB中点M为（-2，1），|AB|=4
3
，求直线l的方程和椭圆方程．
已知向量
m
=（cos（x-
π
6
），0），
n
=（2，0），x∈R，函数f（x）=
m
•
n
．
（1）求函数f（x）的表达式；
（2）求f（π）的值；
（3）若f（α+
2π
3
）=
6
5
，α∈（-
π
2
，0），求f（2α）的值．
设
a
，
b
为向量，若
a
+
b
与
a
的夹角为
π
3
，
a
+
b
与
b
的夹角为
π
4
，则
|
a
|
|
b
|
=
 
．
已知双曲线
x2
a2
-
y2
4
=1（a＞0）的一条渐近线与圆（x-3）2+y2=8相交于M，N两点且|MN|=4，则此双曲线的离心率为（　　）
A、
5
B、
3
5
5
C、
5
5
3
D、5
已知函数f（x）=ex+ax（a∈R），g（x）=exlnx（e为自然对数的底数）．
（Ⅰ）设曲线y=f（x）在x=1处的切线为l，点（1，0）到直线l的距离为
2
2
，求a的值；
（Ⅱ）若对于任意实数x≥0，f（x）＞0恒成立，试确定实数a的取值范围；
（Ⅲ）当a=-1时，函数M（x）=g（x）-f（x）在[1，e]上是否存在极值？若存在，求出极值；若不存在，请说明理由．

违法和不良信息举报电话：027-86699610 举报邮箱：58377363@163.com

精英家教网