题目内容

已知点A（4，0）、B（0，4）、C（3cosα，3sinα）．
（1）若α∈（0，π），且|
AC
|=|
BC
|，求α的大小；
（2）
AC
⊥
BC
，求
2sin2α+sin2α
1+tanα
的值．
考点：三角函数的化简求值,向量的模
专题：三角函数的求值
分析：（1）直接利用|
AC
|=|
BC
|，列出方程求出α的正切函数值，然后求解α的大小；
（2）通过
AC
⊥
BC
，得到α的三角函数值，化简
2sin2α+sin2α
1+tanα
求解即可．
解答： 解：（1）点A（4，0）、B（0，4）、C（3cosα，3sinα）．
α∈（0，π），且|
AC
|=|
BC
|，
可得：（3cosα-4）2+（3sinα-0）2=（3cosα）2+（3sinα-4）2，
可得：-24cosα=-24sinα，
即tanα=1，∴α=
π
4

（2）
AC
=（3cosα-4，3sinα），
BC
=（3cosα，3sinα-4），
AC
⊥
BC
，可得：9cos2α-12cosα+9sin2α-12sinα=0，sinα+cosα=
3
4
．
∴1+2sinαcosα=
9
16
，∴2sinαcosα=-
7
16

2sin2α+sin2α
1+tanα
=
2sinα(sinα+cosα)cosα
cosα+sinα
=2sinαcosα=-
7
16
点评：本题考查两角和与差的三角函数，弦切互化，三角函数的化简求值，考查计算能力．
练习册系列答案
相关题目
函数f（x）=（
1
4
）x+（
1
2
）x-1，x∈[0，+∞）的值域为（　　）
A、（-
5
4
，1]
B、[-
5
4
，1]
C、（-1，1]
D、[-1，1]
下列函数中，其图象关于x=
5
6
π对称的是（　　）
A、y=sin（x-
π
3
）
B、y=sin（x-
5
6
π）
C、y=sin（x+
π
6
）
D、y=sin（x+
π
3
）
设a∈R，且（a+i）2i为正实数，则a=（　　）
A、1B、0C、-1D、0或-1
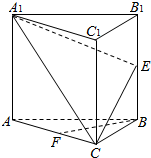如图，在正三棱柱ABC-A1B1C1中，E，F分别为BB1，AC的中点．
（1）求证：BF∥平面A1EC；
（2）若AB=AA1=2，求点A到平面A1EC的距离．
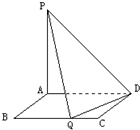如图所示，矩形ABCD的边AB=a，BC=2，PA⊥平面ABCD，PA=2，现有数据：
①a=
3
2
；②a=1；③a=
3
；④a=2；⑤a=4；
（1）当在BC边上存在点Q，使PQ⊥QD时，a可能取所给数据中的哪些值？请说明理由；
（2）在满足（1）的条件下，a取所给数据中的最大值时，求直线PQ与平面ADP所成角的正值；
（3）记满足（1）的条件下的Q点为Qn（n=1，2，3，…），若a取所给数据的最小值时，这样的Q有几个？试求二面角Qn-PA-Qn+1的大小．
已知直线l过点（-1，0），当直线l与圆x2+y2=2x有两个交点时，其斜率k的取值范围是（　　）
A、（-
2
，
3
）
B、（-
2
，
2
）
C、（-1，1）
D、（-
3
3
，
3
3
）
某企业生产一种产品，由于受技术水平的限制，会产生一些次品，根据经验，其次品率Q与日产量x（万件）之间大体满足关系：Q=
1
2(12-x)
，1≤x≤a
1
2
，a＜x≤11
，（其中a为常数，且1＜a＜11）．
（注：次品率=次品数/生产量，如P=0.1表示每生产10件产品，有1件为次品，其余为合格品）．已知每生产1万件合格的产品可以盈利2万元，但每生产1万件次品将亏损1万元．
（Ⅰ）试将生产这种产品每天的盈利额P（x）（万元）表示为日产量x（万件）的函数；
（Ⅱ）当日产量为多少时，可获得最大利润？
在△ABC中，已知A（3，-1），∠B的内角平分线所在的直线的方程是x+y-8=0，AB边上中线所在的直线的方程是x-3y+3=0，求BC边所在直线的方程．

违法和不良信息举报电话：027-86699610 举报邮箱：58377363@163.com

精英家教网