题目内容
函数f(x)=(
)x+(
)x-1,x∈[0,+∞)的值域为( )
| 1 |
| 4 |
| 1 |
| 2 |
A、(-
| ||
B、[-
| ||
| C、(-1,1] | ||
| D、[-1,1] |
考点:指数型复合函数的性质及应用
专题:计算题,函数的性质及应用
分析:令t=(
)x(0<t≤1),则y=t2+t-1=(t+
)2-
,由y在(0,1]递增,计算即可得到值域.
| 1 |
| 2 |
| 1 |
| 2 |
| 5 |
| 4 |
解答:
解:令t=(
)x(0<t≤1),
则y=t2+t-1=(t+
)2-
,且在(0,1]递增,
则有-1<y≤1,
则值域为(-1,1].
故选C.
| 1 |
| 2 |
则y=t2+t-1=(t+
| 1 |
| 2 |
| 5 |
| 4 |
则有-1<y≤1,
则值域为(-1,1].
故选C.
点评:本题考查指数函数的单调性的运用,考查换元法和二次函数的值域求法,考查运算能力,属于基础题.

练习册系列答案
 阅读快车系列答案
阅读快车系列答案
相关题目
2lg2+lg25=( )
| A、1 | B、2 | C、10 | D、100 |
四棱锥P-ABCD的底面与侧面的形状和大小如图所示.
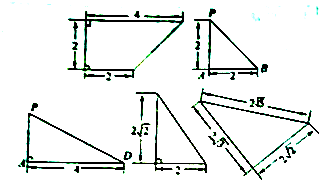
(1)画出该四棱锥的直观图,并证明:当E为PA的中点时,BE∥平面PCD;
(2)若从该四棱锥的8条棱中,任取2条棱,则恰好满足相互垂直的概率是多少?

(1)画出该四棱锥的直观图,并证明:当E为PA的中点时,BE∥平面PCD;
(2)若从该四棱锥的8条棱中,任取2条棱,则恰好满足相互垂直的概率是多少?
设I={2,4,a2-a-3},A={4,1-a},若∁IA={-1},则a=( )
| A、2 | B、-1 | C、0 | D、-1或2 |