题目内容
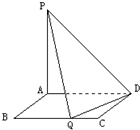 如图所示,矩形ABCD的边AB=a,BC=2,PA⊥平面ABCD,PA=2,现有数据:
如图所示,矩形ABCD的边AB=a,BC=2,PA⊥平面ABCD,PA=2,现有数据:①a=
| ||
| 2 |
| 3 |
(1)当在BC边上存在点Q,使PQ⊥QD时,a可能取所给数据中的哪些值?请说明理由;
(2)在满足(1)的条件下,a取所给数据中的最大值时,求直线PQ与平面ADP所成角的正值;
(3)记满足(1)的条件下的Q点为Qn(n=1,2,3,…),若a取所给数据的最小值时,这样的Q有几个?试求二面角Qn-PA-Qn+1的大小.
考点:用空间向量求平面间的夹角,直线与平面垂直的性质,直线与平面所成的角
专题:空间位置关系与距离,空间角
分析:建立如图所示的空间直角坐标系,求出相关点的坐标
(1)求出
=(a,x,-2),
=(-a,2-x,0)利用
•
=0,求出a即可.
(2)求出
以及平面ADP的一个法向量,通过向量的数量积求解PQ与平面ADP所成角.
(3)判断∠Q1AQ2就是二面角Q1-PA-Q2的平面角.利用cos<
,
>,求解二面角Q1-PA-Q2的大小.
(1)求出
| PQ |
| QD |
| PQ |
| QD |
(2)求出
| PQ |
(3)判断∠Q1AQ2就是二面角Q1-PA-Q2的平面角.利用cos<
| AQ1 |
| AQ2 |
解答:
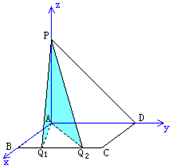 解:建立如图所示的空间直角坐标系,则各点坐标分别为:
解:建立如图所示的空间直角坐标系,则各点坐标分别为:
A(0,0,0,),B(a,0,0),C(a,2,0),D(0,2,0),P(0,0,2),设Q(a,x,0).(0≤x≤2)
(1)∵
=(a,x,-2),
=(-a,2-x,0)
∴由PQ⊥QD得
•
=0,即-a2+2(2-x)=0,解得:a2=x(2-x)
∵x∈[0,2],a2=x(2-x)∈(0,1],
∴在所给数据中,a可取a=
和a=1两个值.
(2)由(1)知a=1,此时x=1,即Q为BC中点,∴点Q的坐标为(1,1,0)
从而
=(1,1,-2),又
=(1,0,0)为平面ADP的一个法向量,
∴cos<
,
>=
=
=
,sin<
,
>=
,
∴PQ与平面ADP所成角的正切值为
.
(3)由(1)知a=
,此时x=
或x=
,即满足条件的点Q有两个,
其坐标为Q1(
,
,0),Q2(
,
,0),
PA⊥平面ABCD,∴PA⊥AQ1,PA⊥AQ2,∴∠Q1AQ2就是二面角Q1-PA-Q2的平面角.
由cos<
,
>=
=
=
,得∠Q1AQ2=30°,
∴二面角Q1-PA-Q2的大小为30°.
 解:建立如图所示的空间直角坐标系,则各点坐标分别为:
解:建立如图所示的空间直角坐标系,则各点坐标分别为:A(0,0,0,),B(a,0,0),C(a,2,0),D(0,2,0),P(0,0,2),设Q(a,x,0).(0≤x≤2)
(1)∵
| PQ |
| QD |
∴由PQ⊥QD得
| PQ |
| QD |
∵x∈[0,2],a2=x(2-x)∈(0,1],
∴在所给数据中,a可取a=
| ||
| 2 |
(2)由(1)知a=1,此时x=1,即Q为BC中点,∴点Q的坐标为(1,1,0)
从而
| PQ |
| AB |
∴cos<
| PQ |
| AB |
| ||||
|
|
| 1 | ||
|
| ||
| 6 |
| PQ |
| AB |
| ||
| 6 |
∴PQ与平面ADP所成角的正切值为
| ||
| 5 |
(3)由(1)知a=
| ||
| 2 |
| 1 |
| 2 |
| 3 |
| 2 |
其坐标为Q1(
| ||
| 2 |
| 1 |
| 2 |
| ||
| 2 |
| 3 |
| 2 |
PA⊥平面ABCD,∴PA⊥AQ1,PA⊥AQ2,∴∠Q1AQ2就是二面角Q1-PA-Q2的平面角.
由cos<
| AQ1 |
| AQ2 |
| ||||
|
|
| ||||
1×
|
| ||
| 2 |
∴二面角Q1-PA-Q2的大小为30°.
点评:本题考查空间向量求解二面角的大小,直线与平面所成角,直线的垂直的判断与应用,考查分析问题解决问题的能力,空间想象能力.

练习册系列答案
 阅读快车系列答案
阅读快车系列答案
相关题目
如图所示,程序框图中输出的结果T是( )


| A、30 | B、31 | C、32 | D、33 |
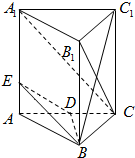 已知三棱柱ABC-A1B1C1中,AB=2,AA1=
已知三棱柱ABC-A1B1C1中,AB=2,AA1=| 3 |
(Ⅰ)当E为AA1中点时,求证:ED∥平面A1B2C
(Ⅱ)当点A到平面BDE的距离为
| 1 |
| 2 |
函数f(x)=
+
-1的定义域为( )
| 1-x |
| x+3 |
| A、(-∞,1] |
| B、[-3,+∞) |
| C、(-∞,-3]∪[1,+∞) |
| D、[-3,1] |