题目内容
设a∈R，且（a+i）2i为正实数，则a=（ ）
| A、1 | B、0 | C、-1 | D、0或-1 |
考点：复数的基本概念
专题：数系的扩充和复数
分析：利用复数的运算法则、复数为实数的条件即可得出．
解答：
解：∵a∈R，且（a+i）2i=（a2-1+2ai）i=-2a+（a2-1）i为正实数，
∴
，解得a=-1．
故选：C．
∴
|
故选：C．
点评：本题考查了复数的运算法则、复数为实数的条件，属于基础题．
练习册系列答案
相关题目
设I={2，4，a2-a-3}，A={4，1-a}，若∁IA={-1}，则a=（ ）
| A、2 | B、-1 | C、0 | D、-1或2 |
如图所示，程序框图中输出的结果T是（ ）
| A、30 | B、31 | C、32 | D、33 |
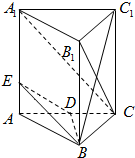已知三棱柱ABC-A1B1C1中，AB=2，AA1=| 3 |
（Ⅰ）当E为AA1中点时，求证：ED∥平面A1B2C
（Ⅱ）当点A到平面BDE的距离为
| 1 |
| 2 |
函数g（x）是偶函数，函数f（x）=g（x-m），若存在φ∈（
，
），使f（sinφ）=f（cosφ），则实数m的取值范围是（ ）
| π |
| 4 |
| π |
| 2 |
A、（
| ||||||
B、（
| ||||||
C、（
| ||||||
D、（
|