题目内容
设函数f(x)=ax-
,曲线y=f(x)在点(2,f(2))处的切线方程为7x-4y-12=0.则曲线y=f(x)上任一点处的切线与直线x=0和直线y=x所围成的三角形面积为 .
| b |
| x |
考点:定积分,利用导数研究曲线上某点切线方程
专题:导数的综合应用
分析:已知曲线上的点,并且知道过此点的切线方程,容易求出斜率,又知点(2,f(2))在曲线上,利用方程联立解出a,b;可以设P(x0,y0)为曲线上任一点,得到切线方程,再利用切线方程分别与直线x=0和直线y=x联立,得到交点坐标,接着利用三角形面积公式即可.
解答:
解:因为函数f(x)=ax-
,曲线y=f(x)在点(2,f(2))处的切线方程为7x-4y-12=0.所以f′(x)|x=2=a+
|x=2=
,所以
,解得
,故f(x)=x-
.
设P(x0,y0)为曲线上任一点,由y′=1+
知
曲线在点P(x0,y0)处的切线方程为y-y0=(1+
)(x-x0),
令x=0,得y=-
,从而得切线与直线x=0的交点坐标为(0,-
);
令y=x,得y=x=2x0,从而得切线与直线y=x的交点坐标为(2x0,2x0);
所以点P(x0,y0)处的切线与直线x=0,y=x所围成的三角形面积为
|-
||2x0|=6.
故曲线y=f(x)上任一点处的切线与直线x=0,y=x所围成的三角形面积为定值,此定值为6.
故答案为:6.
| b |
| x |
| b |
| x2 |
| 7 |
| 4 |
|
|
| 3 |
| x |
设P(x0,y0)为曲线上任一点,由y′=1+
| 3 |
| x2 |
曲线在点P(x0,y0)处的切线方程为y-y0=(1+
| 3 |
| x02 |
令x=0,得y=-
| 6 |
| x0 |
| 6 |
| x0 |
令y=x,得y=x=2x0,从而得切线与直线y=x的交点坐标为(2x0,2x0);
所以点P(x0,y0)处的切线与直线x=0,y=x所围成的三角形面积为
| 1 |
| 2 |
| 6 |
| x0 |
故曲线y=f(x)上任一点处的切线与直线x=0,y=x所围成的三角形面积为定值,此定值为6.
故答案为:6.
点评:本题考查了导数及直线方程、三角形面积的相关知识,运算量较大,属于中档题

练习册系列答案
 通城学典默写能手系列答案
通城学典默写能手系列答案 金牌教辅培优优选卷期末冲刺100分系列答案
金牌教辅培优优选卷期末冲刺100分系列答案
相关题目
在边长为1的等边△ABC中,D,E分别在边BC与AC上,且
=
,2
=
,则
•
=( )
| BD |
| DC |
| AE |
| EC |
| AD |
| BE |
A、-
| ||
B、-
| ||
C、-
| ||
D、-
|
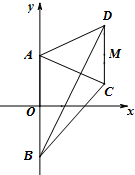 如图,梯形ABCD的底边AB在y轴上,原点O为AB的中点,|AB|=
如图,梯形ABCD的底边AB在y轴上,原点O为AB的中点,|AB|= 函数f(x)=3sin(2x+
函数f(x)=3sin(2x+