Question

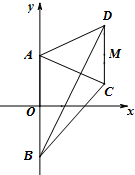如图，梯形ABCD的底边AB在y轴上，原点O为AB的中点，|AB|=

4 2

3

，|CD|=2-

4 2

3

，AC⊥BD，M为CD的中点．
（1）求点M的轨迹方程；
（2）过M作AB的垂线，垂足为N，若存在正常数λ₀，使

MP

=λ0

PN

，且P点到A、B 的距离和为定值，求点P的轨迹E的方程；
（3）过(0，

1

2

)的直线与轨迹E交于P、Q两点，求△OPQ面积的最大值．

Answer 1

考点：轨迹方程

专题：向量与圆锥曲线,圆锥曲线的定义、性质与方程

分析：（1）由题意设出M的坐标，得到C，D的坐标，由

AC

•

BD

=0列式得到M的轨迹方程；
（2）设出P的坐标，得到M的坐标，把M的坐标代入（1）中的轨迹方程即可求得P的轨迹；
（3）设出直线l的方程，和椭圆方程联立，利用根与系数的关系求得P，Q两点横坐标差的绝对值，代入三角形的面积后换元，然后利用配方法求得最值．

解答： 解：（1）设点M的坐标为M（x，y）（x≠0），则C(x，y-1+

2

3

2

)，D(x，y+1-

2

3

2

)．
又A(0，

2 2

3

)，B(0，-

2

3

2

)．
由AC⊥BD，有

AC

•

BD

=0，即（x，y-1）•（x，y+1）=0，
∴x²+y²=1（x≠0）；
（2）设P（x，y），则M（（1+λ₀）x，y），代入M的轨迹方程有(1+λ0)2x2+y2=1(x≠0)．
即

x2

( 1 1+λ0 )2

+y2=1(x≠0)，
∴P的轨迹为椭圆（除去长轴的两个端点）．
要P到A、B的距离之和为定值，则以A、B为焦点，故1-

1

(1+λ0)2

=(

2

3

2

)2．
∴λ₀=2．
从而所求P的轨迹方程为9x²+y²=1（x≠0）；
（3）由题意知l的斜率存在，设方程为y=kx+

1

2

．
联立9x²+y²=1，有(9+k2)x2+kx-

3

4

=0．
设P（x₁，y₁），Q（x₂，y₂），
则x1+x2=-

k

9+k2

，x1x2=

-3

4(9+k2)

．
∴|x2-x1|=

(x1+x2)2-4x1x2

=

4k2+27 (9+k2)2

．
令t=k²+9，则|x2-x1|=

4t-9 t2

，且t≥9．
∴S△OPQ=

1

2

×

1

2

|x2-x1|=

1

4

-9× 1 t2 +4× 1 t

=

1

4

-9( 1 t - 2 9 )2+ 4 9

，
∵t≥9，
∴0＜

1

t

≤

1

9

．
∴当

1

t

=

1

9

，即t=9，也即k=0时，△OPQ面积取最大值，最大值为

3

12

．

点评：本题考查了利用向量法求曲线的轨迹方程，考查了椭圆的定义，训练了直线与圆锥曲线间的关系，涉及直线与圆锥曲线的关系问题，常用直线与圆锥曲线联立，利用根与系数的关系解题，考查了学生的计算能力，是压轴题．