题目内容
3.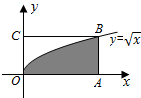 如图,函数$y=\sqrt{x}$的图象过矩形OABC的顶点B,且OA=4.若在矩形OABC内随机地撒100粒豆子,落在图中阴影部分的豆子有67粒,则据此可以估算出图中阴影部分的面积约为( )
如图,函数$y=\sqrt{x}$的图象过矩形OABC的顶点B,且OA=4.若在矩形OABC内随机地撒100粒豆子,落在图中阴影部分的豆子有67粒,则据此可以估算出图中阴影部分的面积约为( )| A. | 2.64 | B. | 2.68 | C. | 5.36 | D. | 6.64 |
分析 由题意,AB=2,SOABC=8,符合几何概型,从而可得$\frac{S}{8}=\frac{67}{100}$,即可求解.
解答 解:由题意,AB=2,SOABC=8,符合几何概型,
设阴影部分的面积为S,
则$\frac{S}{8}=\frac{67}{100}$,解得S=5.36,
故选:C.
点评 本题考查了几何概型的应用及频率估计概率的思想应用,属于基础题.

练习册系列答案
相关题目
14.已知函数$f(x)=Asin({ωx+φ})({A>0,ω>0,|φ|<\frac{π}{2}})$的部分图象如图所示,则下列判断错误的是( )
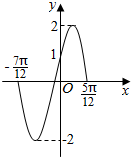

| A. | ω=2 | |
| B. | $f({\frac{π}{3}})=1$ | |
| C. | 函数f(x)的图象关于(-$\frac{11π}{12}$,0)对称 | |
| D. | 函数f(x)的图象向左平移$\frac{11π}{12}$个单位后得到y=Asinωx的图象 |
8.已知命题p:?x>0,总有2x>1,则¬p为( )
| A. | ?x>0,总有2x≤1 | B. | ?x≤0,总有2x≤1 | ||
| C. | $?{x_0}≤0,使得{2^{x_0}}≤1$ | D. | $?{x_0}>0,使得{2^{x_0}}≤1$ |
15.已知函数f(2x-1)的定义域为[-1,4],则函数f(x)的定义域为( )
| A. | (-3,7] | B. | [-3,7] | C. | (0,$\frac{5}{2}$] | D. | [0,$\frac{5}{2}$) |
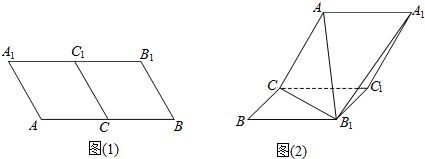
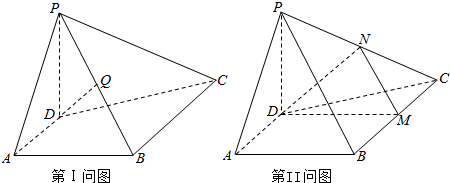
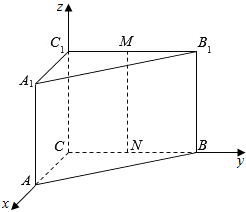 在直三棱柱ABC-A1B1C1中,AC=2,CB=CC1=4,∠BCA=90°,E、F、M、N分别是A1B1、AB、C1B1、CB的中点,建立如图所示的坐标系.
在直三棱柱ABC-A1B1C1中,AC=2,CB=CC1=4,∠BCA=90°,E、F、M、N分别是A1B1、AB、C1B1、CB的中点,建立如图所示的坐标系.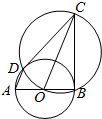 如图所示,直径分别为AB、OC的两圆相交于B、D两点,O为AB的中点.
如图所示,直径分别为AB、OC的两圆相交于B、D两点,O为AB的中点.