题目内容
15．已知函数f（2x-1）的定义域为[-1，4]，则函数f（x）的定义域为（ ）| A． | （-3，7] | B． | [-3，7] | C． | （0，$\frac{5}{2}$] | D． | [0，$\frac{5}{2}$） |
分析 由函数f（2x-1）的定义域为[-1，4]，即x∈[-1，4]，求得2x-1的范围得答案．
解答 解：∵函数f（2x-1）的定义域为[-1，4]，
即-1≤x≤4，
∴-3≤2x-1≤7，
即函数f（x）的定义域为[-3，7]．
故选：B．
点评 本题考查函数的定义域及其求法，关键是掌握该类问题的解决方法，是基础题．
练习册系列答案
小学教材全测系列答案
小学数学口算题卡脱口而出系列答案
优秀生应用题卡口算天天练系列答案
浙江之星课时优化作业系列答案
相关题目
8．在Rt△ABC中，∠ACB=90°，AC=1，BC=2，CD是∠ACB的角平分线（如图①）．若沿直线CD将△ABC折成直二面角B-CD-A（如图②）．则折叠后A，B两点间的距离为（ ）
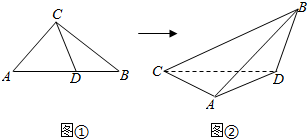
| A． | $\sqrt{2}$ | B． | $\sqrt{3}$ | C． | 2 | D． | 3 |
9．已知函数f（x）=|2x-$\frac{a}{{2}^{x}}$|，其在区间[0，1]上单调递增，则a的取值范围为（ ）
| A． | [0，1] | B． | [-1，0] | C． | [-1，1] | D． | [-$\frac{1}{2}$，$\frac{1}{2}$] |
3．
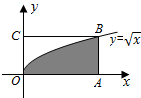如图，函数$y=\sqrt{x}$的图象过矩形OABC的顶点B，且OA=4．若在矩形OABC内随机地撒100粒豆子，落在图中阴影部分的豆子有67粒，则据此可以估算出图中阴影部分的面积约为（ ）
如图，函数$y=\sqrt{x}$的图象过矩形OABC的顶点B，且OA=4．若在矩形OABC内随机地撒100粒豆子，落在图中阴影部分的豆子有67粒，则据此可以估算出图中阴影部分的面积约为（ ）| A． | 2.64 | B． | 2.68 | C． | 5.36 | D． | 6.64 |
20．阅读如图所示的程序框图，该程序输出的结果是（ ）
| A． | 95 | B． | 94 | C． | 93 | D． | 92 |
7．如果实数x，y满足条件$\left\{\begin{array}{l}{x-2y+2≥0}\\{2x-y-2≤0}\\{x+y-1≥0}\end{array}\right.$，則z=3x-2y的最小值为（ ）
| A． | -4 | B． | -2 | C． | 1 | D． | 2 |
4．已知点M（-4，0），N（4，0），B（2，0），动圆C与直线MN切于点B，过M、N与圆C相切的两直线相交于点P，则P点的轨迹方程是（ ）
| A． | $\frac{{x}^{2}}{4}$-$\frac{{y}^{2}}{12}$=1（x＞2） | B． | $\frac{{x}^{2}}{4}$-$\frac{{y}^{2}}{12}$=1（x＜-2） | ||
| C． | $\frac{{x}^{2}}{4}$-$\frac{{y}^{2}}{12}$=1（x≠±2） | D． | $\frac{{x}^{2}}{4}$+$\frac{{y}^{2}}{12}$=1（x≠±2） |