题目内容
14.已知函数$f(x)=Asin({ωx+φ})({A>0,ω>0,|φ|<\frac{π}{2}})$的部分图象如图所示,则下列判断错误的是( )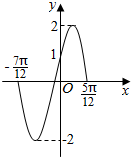
| A. | ω=2 | |
| B. | $f({\frac{π}{3}})=1$ | |
| C. | 函数f(x)的图象关于(-$\frac{11π}{12}$,0)对称 | |
| D. | 函数f(x)的图象向左平移$\frac{11π}{12}$个单位后得到y=Asinωx的图象 |
分析 由函数的最值求出A,由周期求出ω,由特殊点的坐标求出φ的值,再根据y=Asin(ωx+φ)的图象变换规律,从而得出结论.
解答 解:根据函数$f(x)=Asin({ωx+φ})({A>0,ω>0,|φ|<\frac{π}{2}})$的部分图象如图所示,
可知,A=2,$T=\frac{5π}{12}+\frac{7π}{12}=π$,∴$ω=\frac{2π}{π}=2$,
再根据f(0)=Asinφ=2sinφ=1,且$|φ|<\frac{π}{2}$,∴$φ=\frac{π}{6}$,∴$f(x)=2sin({2x+\frac{π}{6}})$,
∴$f({\frac{π}{3}})=2sin\frac{5π}{6}=1,f({-\frac{11π}{12}})≠0$,故函数f(x)的图象不关于$({-\frac{11π}{12},0})$对称,
易得f(x)的图象向右平移$\frac{π}{12}$个单位后得到y=Asinωx的图象,
故选:C.
点评 本题主要考查利用y=Asin(ωx+φ)的图象特征,由函数y=Asin(ωx+φ)的部分图象求解析式,由函数的最值求出A,由周期求出ω,由特殊点的坐标求出φ的值,y=Asin(ωx+φ)的图象变换规律,属于基础题.

练习册系列答案
 名校课堂系列答案
名校课堂系列答案
相关题目
9.已知函数f(x)=|2x-$\frac{a}{{2}^{x}}$|,其在区间[0,1]上单调递增,则a的取值范围为( )
| A. | [0,1] | B. | [-1,0] | C. | [-1,1] | D. | [-$\frac{1}{2}$,$\frac{1}{2}$] |
3.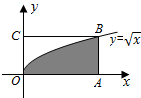 如图,函数$y=\sqrt{x}$的图象过矩形OABC的顶点B,且OA=4.若在矩形OABC内随机地撒100粒豆子,落在图中阴影部分的豆子有67粒,则据此可以估算出图中阴影部分的面积约为( )
如图,函数$y=\sqrt{x}$的图象过矩形OABC的顶点B,且OA=4.若在矩形OABC内随机地撒100粒豆子,落在图中阴影部分的豆子有67粒,则据此可以估算出图中阴影部分的面积约为( )
 如图,函数$y=\sqrt{x}$的图象过矩形OABC的顶点B,且OA=4.若在矩形OABC内随机地撒100粒豆子,落在图中阴影部分的豆子有67粒,则据此可以估算出图中阴影部分的面积约为( )
如图,函数$y=\sqrt{x}$的图象过矩形OABC的顶点B,且OA=4.若在矩形OABC内随机地撒100粒豆子,落在图中阴影部分的豆子有67粒,则据此可以估算出图中阴影部分的面积约为( )| A. | 2.64 | B. | 2.68 | C. | 5.36 | D. | 6.64 |
20.阅读如图所示的程序框图,该程序输出的结果是( )


| A. | 95 | B. | 94 | C. | 93 | D. | 92 |
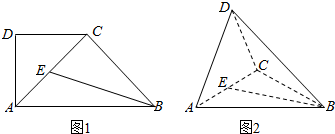 如图1,在直角梯形ABCD中,∠ADC=90°,CD∥AB,AD=CD=$\frac{1}{2}$AB=2,点E为AC中点.将△ADC沿AC折起,使平面ADC⊥平面ABC,得到几何体D-ABC,如图2所示.
如图1,在直角梯形ABCD中,∠ADC=90°,CD∥AB,AD=CD=$\frac{1}{2}$AB=2,点E为AC中点.将△ADC沿AC折起,使平面ADC⊥平面ABC,得到几何体D-ABC,如图2所示.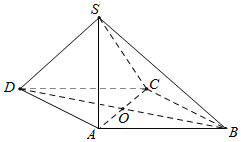 如图所示,四边形ABCD是菱形,O是AC与BD的交点,SA⊥平面ABCD
如图所示,四边形ABCD是菱形,O是AC与BD的交点,SA⊥平面ABCD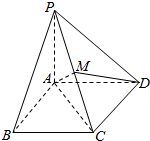 如图,已知四棱锥P-ABCD中,PA⊥底面ABCD,且ABCD为正方形,PA=AB=a,点M是PC的中点.
如图,已知四棱锥P-ABCD中,PA⊥底面ABCD,且ABCD为正方形,PA=AB=a,点M是PC的中点.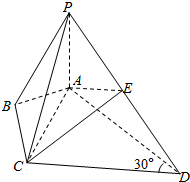 在四棱锥P-ABCD中,∠ABC=∠ACD=90°,∠BAC=∠CAD=60°,E为PD的中点.
在四棱锥P-ABCD中,∠ABC=∠ACD=90°,∠BAC=∠CAD=60°,E为PD的中点.