题目内容
12.设全集U=R,集合A={x|-1≤x<3},B={x|2x-4≤x-2}.(Ⅰ)求A∩(∁UR);
(Ⅱ)若函数f(x)=lg(2x+a)的定义域为集合C,满足A⊆C,求实数a的取值范围.
分析 (Ⅰ)求出∁UB,即可求A∩(∁UB);
(Ⅱ)求出集合C,利用A⊆C,即可求实数a的取值范围.
解答 解:(Ⅰ)B={x|x≤2}.
∴∁UB={x|x>2}
∴A∩(∁UB)={x|2<x<3};
(Ⅱ)函数f(x)=lg(2x+a)的定义域为集合C={x|x>-$\frac{a}{2}$},
∵A⊆C,
∴-$\frac{a}{2}$<-1,
∴a>2.
点评 本题考查集合的关系与运算,考查学生的计算能力,属于中档题.

练习册系列答案
 走进文言文系列答案
走进文言文系列答案
相关题目
3.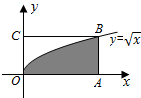 如图,函数$y=\sqrt{x}$的图象过矩形OABC的顶点B,且OA=4.若在矩形OABC内随机地撒100粒豆子,落在图中阴影部分的豆子有67粒,则据此可以估算出图中阴影部分的面积约为( )
如图,函数$y=\sqrt{x}$的图象过矩形OABC的顶点B,且OA=4.若在矩形OABC内随机地撒100粒豆子,落在图中阴影部分的豆子有67粒,则据此可以估算出图中阴影部分的面积约为( )
 如图,函数$y=\sqrt{x}$的图象过矩形OABC的顶点B,且OA=4.若在矩形OABC内随机地撒100粒豆子,落在图中阴影部分的豆子有67粒,则据此可以估算出图中阴影部分的面积约为( )
如图,函数$y=\sqrt{x}$的图象过矩形OABC的顶点B,且OA=4.若在矩形OABC内随机地撒100粒豆子,落在图中阴影部分的豆子有67粒,则据此可以估算出图中阴影部分的面积约为( )| A. | 2.64 | B. | 2.68 | C. | 5.36 | D. | 6.64 |
20.阅读如图所示的程序框图,该程序输出的结果是( )


| A. | 95 | B. | 94 | C. | 93 | D. | 92 |
7.如果实数x,y满足条件$\left\{\begin{array}{l}{x-2y+2≥0}\\{2x-y-2≤0}\\{x+y-1≥0}\end{array}\right.$,則z=3x-2y的最小值为( )
| A. | -4 | B. | -2 | C. | 1 | D. | 2 |
4.已知点M(-4,0),N(4,0),B(2,0),动圆C与直线MN切于点B,过M、N与圆C相切的两直线相交于点P,则P点的轨迹方程是( )
| A. | $\frac{{x}^{2}}{4}$-$\frac{{y}^{2}}{12}$=1(x>2) | B. | $\frac{{x}^{2}}{4}$-$\frac{{y}^{2}}{12}$=1(x<-2) | ||
| C. | $\frac{{x}^{2}}{4}$-$\frac{{y}^{2}}{12}$=1(x≠±2) | D. | $\frac{{x}^{2}}{4}$+$\frac{{y}^{2}}{12}$=1(x≠±2) |
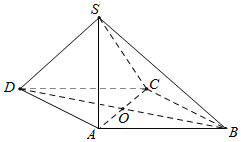 如图所示,四边形ABCD是菱形,O是AC与BD的交点,SA⊥平面ABCD
如图所示,四边形ABCD是菱形,O是AC与BD的交点,SA⊥平面ABCD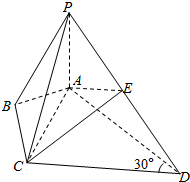 在四棱锥P-ABCD中,∠ABC=∠ACD=90°,∠BAC=∠CAD=60°,E为PD的中点.
在四棱锥P-ABCD中,∠ABC=∠ACD=90°,∠BAC=∠CAD=60°,E为PD的中点.