题目内容
19.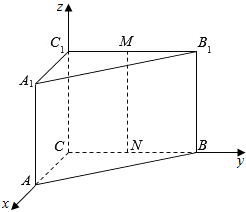 在直三棱柱ABC-A1B1C1中,AC=2,CB=CC1=4,∠BCA=90°,E、F、M、N分别是A1B1、AB、C1B1、CB的中点,建立如图所示的坐标系.
在直三棱柱ABC-A1B1C1中,AC=2,CB=CC1=4,∠BCA=90°,E、F、M、N分别是A1B1、AB、C1B1、CB的中点,建立如图所示的坐标系.(1)在平面ABB1A1内找一点P,使△ABP为正三角形;
(2)能否在MN上求得点Q,使△AQB为以AB为斜边的直角三角形?若能,请求出点Q的坐标;若不能,请说明理由.
分析 (1)由已知可得P的横纵坐标与AB中点的横纵坐标相等,竖坐标的绝对值等于正三角形的高,进而得到答案;
(2)若△AQB为以AB为斜边的直角三角形,则$\overrightarrow{AQ}$•$\overrightarrow{BQ}$=0,进而得到答案;
解答 解:(1)直三棱柱ABC-A1B1C1中,AC=2,CB=CC1=4,∠BCA=90°,
故AB=$\sqrt{{AC}^{2}{+CB}^{2}}$=2$\sqrt{5}$,
若△ABP为正三角形,则P到AB的距离为正三角形的高:2$\sqrt{5}$×$\frac{\sqrt{3}}{2}$=$\sqrt{15}$,
又由P在平面ABB1A1内,
故P的横纵坐标与AB中点的横纵坐标相等,竖坐标的绝对值等于正三角形的高,
∵AC=2,CB=4,
故AB中点坐标为(1,2,0),
故P点坐标为:(1,2,±$\sqrt{15}$);
(2)设Q点的坐标为(0,2,z),
则$\overrightarrow{AQ}$=(-2,2,z),$\overrightarrow{BQ}$=(0,-2,z),
若△AQB为以AB为斜边的直角三角形,
则$\overrightarrow{AQ}$•$\overrightarrow{BQ}$=0,
即Z2=4,
解得:z=2,或z=-2(舍去),
故Q点的坐标为(0,2,2)
点评 本题考查的知识点是向量数量积判断向量的垂直,等边三角形的性质,难度中档.

练习册系列答案
 名校课堂系列答案
名校课堂系列答案
相关题目
12.执行如图的框图,若输入k=30,则输出的n=( )


| A. | 4 | B. | 5 | C. | 6 | D. | 7 |
9.已知函数f(x)=|2x-$\frac{a}{{2}^{x}}$|,其在区间[0,1]上单调递增,则a的取值范围为( )
| A. | [0,1] | B. | [-1,0] | C. | [-1,1] | D. | [-$\frac{1}{2}$,$\frac{1}{2}$] |
16.设集合A={x|x2-x-2<0},B={x|-1<x<1},则( )
| A. | A?B | B. | B⊆A | C. | A=B | D. | A∩B=∅ |
3.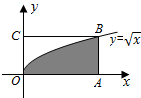 如图,函数$y=\sqrt{x}$的图象过矩形OABC的顶点B,且OA=4.若在矩形OABC内随机地撒100粒豆子,落在图中阴影部分的豆子有67粒,则据此可以估算出图中阴影部分的面积约为( )
如图,函数$y=\sqrt{x}$的图象过矩形OABC的顶点B,且OA=4.若在矩形OABC内随机地撒100粒豆子,落在图中阴影部分的豆子有67粒,则据此可以估算出图中阴影部分的面积约为( )
 如图,函数$y=\sqrt{x}$的图象过矩形OABC的顶点B,且OA=4.若在矩形OABC内随机地撒100粒豆子,落在图中阴影部分的豆子有67粒,则据此可以估算出图中阴影部分的面积约为( )
如图,函数$y=\sqrt{x}$的图象过矩形OABC的顶点B,且OA=4.若在矩形OABC内随机地撒100粒豆子,落在图中阴影部分的豆子有67粒,则据此可以估算出图中阴影部分的面积约为( )| A. | 2.64 | B. | 2.68 | C. | 5.36 | D. | 6.64 |
7.如果实数x,y满足条件$\left\{\begin{array}{l}{x-2y+2≥0}\\{2x-y-2≤0}\\{x+y-1≥0}\end{array}\right.$,則z=3x-2y的最小值为( )
| A. | -4 | B. | -2 | C. | 1 | D. | 2 |
8.已知数列{an}的前n项和Sn=n2-2n+1,△ABC的三边长之比为a3:a4:a5,则△ABC的最大角的余弦值为( )
| A. | $\frac{\sqrt{2}-\sqrt{6}}{4}$ | B. | -$\frac{1}{2}$ | C. | -$\frac{1}{4}$ | D. | -$\frac{\sqrt{3}}{2}$ |
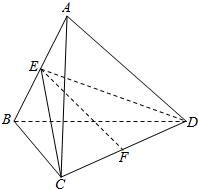 如图,正四面体ABCD的棱长为1.
如图,正四面体ABCD的棱长为1.