题目内容
12. 某制造厂商10月份生产了一批乒乓球,从中随机抽取n个进行检查,测得每个球的直径(单位:mm),将数据进行分组,得到如下频率分布表:
某制造厂商10月份生产了一批乒乓球,从中随机抽取n个进行检查,测得每个球的直径(单位:mm),将数据进行分组,得到如下频率分布表:| 分组 | 频数 | 频率 |
| [39.95,39.97) | 6 | P1 |
| [39.97,39.99) | 12 | 0.20 |
| [39.99,40.01) | a | 0.50 |
| [40.01,40.03) | b | P2 |
| 合计 | n | 1.00 |
(2)已知标准乒乓球的直径为40.00mm,且称直径在[39.99,40.01]内的乒乓球为五星乒乓球,若这批乒乓球共有10000个,试估计其中五星乒乓球的数目.
分析 (1)根据频率=$\frac{频数}{样本容量}$,即可求出答案,并画出图形,
(2)用样本估计总体即可求出答案
解答  解:(1)由n=$\frac{12}{0.2}$=60,
解:(1)由n=$\frac{12}{0.2}$=60,
a=60×0.5=30,p1=$\frac{6}{60}$=0.1,b=60-6-12-30=12,
p2=$\frac{12}{60}$=0.2,
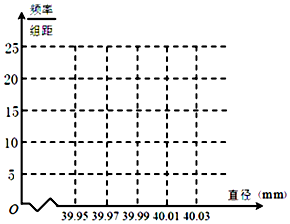
频率分布直方图如图所示:
(2)称直径在[39.99,40.01]内的乒乓球为五星乒乓球的频率为0.5,
于是这批乒乓球共有10000个,可以估计其中五星乒乓球的数目10000×0.5=5000个
点评 本题考查了频率分布表和频率分布直方图,以及用样本估计总体,属于基础题.

练习册系列答案
相关题目
2.给出下列结论:
①命题“?x∈R,sinx≠1”的否定是“?x∈R,sinx=1”;
②数列{an}满足“an+1=3an”是“数列{an}为等比数列”的充分不必要条件;
③命题“若x=y,则sinx=siny”的逆否命题为真命题.
其中正确的是( )
①命题“?x∈R,sinx≠1”的否定是“?x∈R,sinx=1”;
②数列{an}满足“an+1=3an”是“数列{an}为等比数列”的充分不必要条件;
③命题“若x=y,则sinx=siny”的逆否命题为真命题.
其中正确的是( )
| A. | ①②③ | B. | ①③ | C. | ①② | D. | ②③ |
3.设函数f(x)=|2x-a|+|x+a|(a>0).
(1)当a=1时,求f(x)的最小值;
(2)若关于x的不等式$f(x)<\frac{5}{x}+a$在x∈[1,2]上有解,求实数a的取值范围.
(1)当a=1时,求f(x)的最小值;
(2)若关于x的不等式$f(x)<\frac{5}{x}+a$在x∈[1,2]上有解,求实数a的取值范围.
4.用一个平面去截一个四棱锥,截面形状不可能的是( )
| A. | 四边形 | B. | 三角形 | C. | 五边形 | D. | 六边形 |
2.已知cosθ=$\frac{1}{3}$,且θ是第四象限角,则sinθ的值是( )
| A. | -$\frac{1}{3}$ | B. | -$\frac{2\sqrt{2}}{3}$ | C. | $\frac{2\sqrt{2}}{3}$ | D. | $±\frac{2\sqrt{2}}{3}$ |
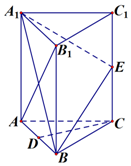 如图,在正三棱柱ABC-A1B1C1中,每条棱长均相等,D为棱AB的中点,E为侧棱CC1的中点.
如图,在正三棱柱ABC-A1B1C1中,每条棱长均相等,D为棱AB的中点,E为侧棱CC1的中点.