题目内容
17.已知直线x-ay+a=0与直线2x+y+2=0平行,则实数a的值为-$\frac{1}{2}$.分析 利用直线x-ay+a=0与直线2x+y+2=0平行,$\frac{1}{2}=\frac{-a}{1}≠\frac{a}{2}$,即可求出a的值.
解答 解:∵直线x-ay+a=0与直线2x+y+2=0平行,
∴$\frac{1}{2}=\frac{-a}{1}≠\frac{a}{2}$,
解得:a=-$\frac{1}{2}$.
故答案为:-$\frac{1}{2}$.
点评 本题考查直线的一般式方程与直线的平行关系,考查解方程的能力,属于中档题.

练习册系列答案
 怎样学好牛津英语系列答案
怎样学好牛津英语系列答案 导学教程高中新课标系列答案
导学教程高中新课标系列答案
相关题目
5.平面α截半径为2的球O所得的截面圆的面积为π,则球心到O平面α的距离为( )
| A. | $\sqrt{3}$ | B. | $\sqrt{2}$ | C. | 1 | D. | 2 |
12. 某制造厂商10月份生产了一批乒乓球,从中随机抽取n个进行检查,测得每个球的直径(单位:mm),将数据进行分组,得到如下频率分布表:
某制造厂商10月份生产了一批乒乓球,从中随机抽取n个进行检查,测得每个球的直径(单位:mm),将数据进行分组,得到如下频率分布表:
(1)求a,b,n及p1,p2的值,并画出频率分布直方图(结果保留两位小数);
(2)已知标准乒乓球的直径为40.00mm,且称直径在[39.99,40.01]内的乒乓球为五星乒乓球,若这批乒乓球共有10000个,试估计其中五星乒乓球的数目.
 某制造厂商10月份生产了一批乒乓球,从中随机抽取n个进行检查,测得每个球的直径(单位:mm),将数据进行分组,得到如下频率分布表:
某制造厂商10月份生产了一批乒乓球,从中随机抽取n个进行检查,测得每个球的直径(单位:mm),将数据进行分组,得到如下频率分布表:| 分组 | 频数 | 频率 |
| [39.95,39.97) | 6 | P1 |
| [39.97,39.99) | 12 | 0.20 |
| [39.99,40.01) | a | 0.50 |
| [40.01,40.03) | b | P2 |
| 合计 | n | 1.00 |
(2)已知标准乒乓球的直径为40.00mm,且称直径在[39.99,40.01]内的乒乓球为五星乒乓球,若这批乒乓球共有10000个,试估计其中五星乒乓球的数目.
2.下列导数公式错误的是( )
| A. | (sinx)'=-cosx | B. | $(lnx)'=\frac{1}{x}$ | C. | $(\frac{1}{x})'=-\frac{1}{x^2}$ | D. | (ex)'=ex |
7.为了解儿子身高与其父亲身高的关系,随机抽取5对父子的身高数据如下:
则y对x的线性回归方程为( )
| 父亲身高x/cm | 174 | 176 | 176 | 176 | 178 |
| 儿子身高y/cm | 175 | 176 | 177 | 178 | 179 |
| A. | $\widehat{y}$=x-1 | B. | $\widehat{y}$=x+1 | C. | $\widehat{y}$=88+$\frac{1}{2}$x | D. | $\widehat{y}$=176 |
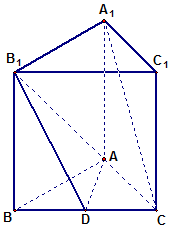 如图,在直三棱柱(侧棱与底面垂直的三棱柱)ABC-A1B1C1中,BB1=8,AB=8,AC=6,BC=10,D是BC边的中点.
如图,在直三棱柱(侧棱与底面垂直的三棱柱)ABC-A1B1C1中,BB1=8,AB=8,AC=6,BC=10,D是BC边的中点.