题目内容
2.已知cosθ=$\frac{1}{3}$,且θ是第四象限角,则sinθ的值是( )| A. | -$\frac{1}{3}$ | B. | -$\frac{2\sqrt{2}}{3}$ | C. | $\frac{2\sqrt{2}}{3}$ | D. | $±\frac{2\sqrt{2}}{3}$ |
分析 利用同角三角函数的基本关系、三角函数在各个象限中的符号,求得sinθ的值.
解答 解:∵知cosθ=$\frac{1}{3}$,且θ是第四象限角,则sinθ=-$\sqrt{{1-cos}^{2}θ}$=-$\frac{2\sqrt{2}}{3}$,
故选:B.
点评 本题主要考查同角三角函数的基本关系的应用,三角函数在各个象限中的符号,属于基础题.

练习册系列答案
 培优口算题卡系列答案
培优口算题卡系列答案 开心口算题卡系列答案
开心口算题卡系列答案 口算题卡河北少年儿童出版社系列答案
口算题卡河北少年儿童出版社系列答案
相关题目
12.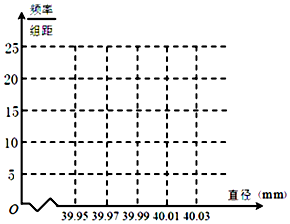 某制造厂商10月份生产了一批乒乓球,从中随机抽取n个进行检查,测得每个球的直径(单位:mm),将数据进行分组,得到如下频率分布表:
某制造厂商10月份生产了一批乒乓球,从中随机抽取n个进行检查,测得每个球的直径(单位:mm),将数据进行分组,得到如下频率分布表:
(1)求a,b,n及p1,p2的值,并画出频率分布直方图(结果保留两位小数);
(2)已知标准乒乓球的直径为40.00mm,且称直径在[39.99,40.01]内的乒乓球为五星乒乓球,若这批乒乓球共有10000个,试估计其中五星乒乓球的数目.
 某制造厂商10月份生产了一批乒乓球,从中随机抽取n个进行检查,测得每个球的直径(单位:mm),将数据进行分组,得到如下频率分布表:
某制造厂商10月份生产了一批乒乓球,从中随机抽取n个进行检查,测得每个球的直径(单位:mm),将数据进行分组,得到如下频率分布表:| 分组 | 频数 | 频率 |
| [39.95,39.97) | 6 | P1 |
| [39.97,39.99) | 12 | 0.20 |
| [39.99,40.01) | a | 0.50 |
| [40.01,40.03) | b | P2 |
| 合计 | n | 1.00 |
(2)已知标准乒乓球的直径为40.00mm,且称直径在[39.99,40.01]内的乒乓球为五星乒乓球,若这批乒乓球共有10000个,试估计其中五星乒乓球的数目.
10.如图中的几何体是由下面哪个三角形绕直线旋转所得到的( )
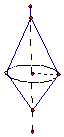

| A. | 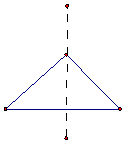 | B. | 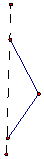 | C. | 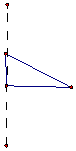 | D. | 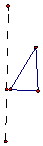 |
7.为了解儿子身高与其父亲身高的关系,随机抽取5对父子的身高数据如下:
则y对x的线性回归方程为( )
| 父亲身高x/cm | 174 | 176 | 176 | 176 | 178 |
| 儿子身高y/cm | 175 | 176 | 177 | 178 | 179 |
| A. | $\widehat{y}$=x-1 | B. | $\widehat{y}$=x+1 | C. | $\widehat{y}$=88+$\frac{1}{2}$x | D. | $\widehat{y}$=176 |
14.已知实数x、y满足$\left\{\begin{array}{l}x-y+2≥0\\ x+y≥0\\ 4x-y-1≤0\end{array}\right.$,则z=2x+y的最大值为( )
| A. | -1 | B. | $\frac{6}{5}$ | C. | 5 | D. | 6 |
11.已知m>1,x,y满足约束条件$\left\{\begin{array}{l}x-y+4≥0\\ mx-y+5-m≤0\\ 0≤x≤1\end{array}$,若目标函数z=ax+by(a>0,b>0)的最大值为3,则$\frac{1}{a}$+$\frac{2}{b}$( )
| A. | 有最小值 $\frac{{11+2\sqrt{10}}}{3}$ | B. | 有最大值$\frac{{11+2\sqrt{10}}}{3}$ | ||
| C. | 有最小值$\frac{{11-2\sqrt{10}}}{3}$ | D. | 有最大值$\frac{{11-2\sqrt{10}}}{3}$ |
12.点P(0,1)到双曲线$\frac{y^2}{4}-{x^2}=1$渐近线的距离是( )
| A. | $\sqrt{5}$ | B. | $\frac{{\sqrt{5}}}{5}$ | C. | $\frac{{2\sqrt{5}}}{5}$ | D. | 5 |
 为了了解高中生的身体健康情况,体育局随机抽取了某校20名学生的体育测试成绩,得到如图所示的茎叶图:
为了了解高中生的身体健康情况,体育局随机抽取了某校20名学生的体育测试成绩,得到如图所示的茎叶图: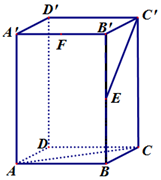 如图长方体ABCD-A'B'C'D'中,AB=BC=1,AA'=2,E、F分别是BB′、A'B'的中点.
如图长方体ABCD-A'B'C'D'中,AB=BC=1,AA'=2,E、F分别是BB′、A'B'的中点.