题目内容
20.已知三棱锥S-ABC的体积为$\frac{\sqrt{2}}{6}$,底面△ABC是边长为1的正三角形,三棱锥S-ABC的所有顶点都在球O的球面上,棱SC是球O的直径,则球O的表面积为4π.分析 根据题意作出图形,欲求球O的表面积,只须求球的半径r.利用截面圆的性质即可求出OO1,进而求出底面ABC上的高SD,即可计算出三棱锥的体积,从而建立关于r的方程,即可求出r,从而解决问题.
解答 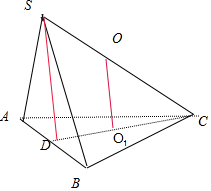 设球心为O,球的半径r.过ABC三点的小圆的圆心为O1,则OO1⊥平面ABC,
设球心为O,球的半径r.过ABC三点的小圆的圆心为O1,则OO1⊥平面ABC,
作SD⊥平面ABC交CO1的延长线与D.$\frac{2}{3}×\frac{\sqrt{3}}{2}=\frac{\sqrt{3}}{3}$,∴OO1=$\sqrt{{R}^{2}-\frac{1}{3}}$,
∴高SD=2OO1,
∵△ABC是边长为1的正三角形,
∴S△ABC=$\frac{\sqrt{3}}{4}$,∴V三棱锥S-ABC=$\frac{1}{3}×2\sqrt{{R}^{2}-\frac{1}{3}}×\frac{\sqrt{3}}{4}=\frac{\sqrt{2}}{6}$,
∴R=1.则球O的表面积为4π,
故答案为:4π.
点评 本题考查棱锥的体积,考查球内接多面体,解题的关键是确定点S到面ABC的距离,属于中档题

练习册系列答案
相关题目
5.平面α截半径为2的球O所得的截面圆的面积为π,则球心到O平面α的距离为( )
| A. | $\sqrt{3}$ | B. | $\sqrt{2}$ | C. | 1 | D. | 2 |
12.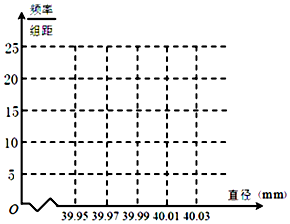 某制造厂商10月份生产了一批乒乓球,从中随机抽取n个进行检查,测得每个球的直径(单位:mm),将数据进行分组,得到如下频率分布表:
某制造厂商10月份生产了一批乒乓球,从中随机抽取n个进行检查,测得每个球的直径(单位:mm),将数据进行分组,得到如下频率分布表:
(1)求a,b,n及p1,p2的值,并画出频率分布直方图(结果保留两位小数);
(2)已知标准乒乓球的直径为40.00mm,且称直径在[39.99,40.01]内的乒乓球为五星乒乓球,若这批乒乓球共有10000个,试估计其中五星乒乓球的数目.
 某制造厂商10月份生产了一批乒乓球,从中随机抽取n个进行检查,测得每个球的直径(单位:mm),将数据进行分组,得到如下频率分布表:
某制造厂商10月份生产了一批乒乓球,从中随机抽取n个进行检查,测得每个球的直径(单位:mm),将数据进行分组,得到如下频率分布表:| 分组 | 频数 | 频率 |
| [39.95,39.97) | 6 | P1 |
| [39.97,39.99) | 12 | 0.20 |
| [39.99,40.01) | a | 0.50 |
| [40.01,40.03) | b | P2 |
| 合计 | n | 1.00 |
(2)已知标准乒乓球的直径为40.00mm,且称直径在[39.99,40.01]内的乒乓球为五星乒乓球,若这批乒乓球共有10000个,试估计其中五星乒乓球的数目.
10.如图中的几何体是由下面哪个三角形绕直线旋转所得到的( )
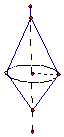

| A. | 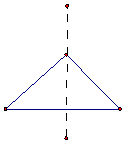 | B. | 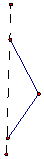 | C. | 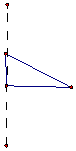 | D. | 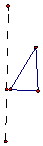 |
 如图,四棱锥P-ABCD,侧面PAD是边长为4的正三角形,且与底面垂直,底面ABCD是∠ABC=60°的菱形,M为PC的中点.
如图,四棱锥P-ABCD,侧面PAD是边长为4的正三角形,且与底面垂直,底面ABCD是∠ABC=60°的菱形,M为PC的中点.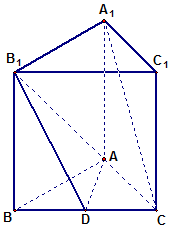 如图,在直三棱柱(侧棱与底面垂直的三棱柱)ABC-A1B1C1中,BB1=8,AB=8,AC=6,BC=10,D是BC边的中点.
如图,在直三棱柱(侧棱与底面垂直的三棱柱)ABC-A1B1C1中,BB1=8,AB=8,AC=6,BC=10,D是BC边的中点.