题目内容
15．已知函数f（x）=$\sqrt{\frac{x+3}{x-2}-2}$的定义域是A，关于x的不等式x2-（a+3）x+3a＜0的解集为B．（1）求集合B；
（2）已知α：x∈A，β：x∈B，若α是β的必要不充分条件，试求实数a的取值范围．
分析 （1）根据一元二次不等式的解法进行求解即可．
（2）根据充分条件和必要条件的定义转化为B?A，利用不等式的关系进行求解即可．
解答 解：（1）由$\frac{x+3}{x-2}$-2≥0得$\frac{7-x}{x-2}$≥0，得2＜x≤7，即A=（2，7]，
由x2-（a+3）x+3a＜0得（x-3）（x-a）＜0，
若a=3，则不等式的解集为B=∅，
若a＞3，则不等式的解集为B=（3，a），
若a＜3，则不等式的解集为B=（a，3）．
（2）若α是β的必要不充分条件，
则B?A，
则当a=3时，满足条件，
若a＞3，则a≤7，此时3＜a≤7，
若a＜3，则a≥2，此时2≤a＜3，
综上，2≤a≤7．
即实数a的取值范围是[2，7]．
点评 本题主要考查一元二次不等式的求解，以及充分条件和必要条件的应用，根据条件进行转化是解决本题的关键．注意要进行分类讨论．
练习册系列答案
相关题目
5．下列函数中，既是奇函数又存在零点的是（ ）
| A． | $y=cos（{\frac{π}{2}-x}）$ | B． | $y=sin（{\frac{π}{2}-x}）$ | C． | y=lnx | D． | $y=x+\frac{1}{x}$ |
6．某四面体的三视图如图所示，该四面体外接球的表面积为（ ）
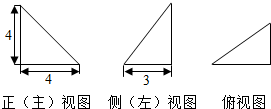
| A． | 41π | B． | $\frac{41π}{2}$ | C． | 48π | D． | 24π |
3．在梯形ABCD中，$\overrightarrow{AB}$=3$\overrightarrow{DC}$，则$\overrightarrow{BC}$等于（ ）
| A． | -$\frac{2}{3}$$\overrightarrow{AB}$+$\overrightarrow{AD}$ | B． | -$\frac{2}{3}$$\overrightarrow{AB}$+$\frac{4}{3}$$\overrightarrow{AD}$ | C． | -$\frac{1}{3}$$\overrightarrow{AB}$+$\frac{2}{3}$$\overrightarrow{AD}$ | D． | -$\frac{2}{3}$$\overrightarrow{AB}$-$\overrightarrow{AD}$ |
4．函数y=f（2x）的定义域为[1，2]，则函数y=f（log2x）的定义域为（ ）
| A． | [0，1] | B． | [1，2] | C． | [2，4] | D． | [4，16] |