题目内容
20.试求出函数y=cos2x-sin2x+2sinxcosx的单调递增区间和最大值.分析 由二倍角公式得到y=sin(2x+$\frac{π}{4}$),由此能求出函数y=cos2x-sin2x+2sinxcosx的单调递增区间和最大值.
解答 解:y=cos2x-sin2x+2sinxcosx
=cos2x+sin2x
=sin(2x+$\frac{π}{4}$),
∴函数y=cos2x-sin2x+2sinxcosx的单调递增区间满足:
-$\frac{π}{2}+2kπ$$≤2x+\frac{π}{4}≤$$\frac{π}{2}+2kπ$,k∈Z,
解得-$\frac{3}{8}π+kπ$≤x≤$\frac{π}{8}+kπ$,
∴函数y=cos2x-sin2x+2sinxcosx的单调递增区间为[-$\frac{3}{8}π+kπ$,$\frac{π}{8}+kπ$],k∈Z;
函数y=cos2x-sin2x+2sinxcosx的最大值为1.
点评 本题考查函数的单调增区间和最大值的求法,是中档题,解题时要认真审题,注意三角函数的性质的合理运用.

练习册系列答案
 黄冈小状元解决问题天天练系列答案
黄冈小状元解决问题天天练系列答案 三点一测快乐周计划系列答案
三点一测快乐周计划系列答案
相关题目
11.给出下列四个命题:
①平行于同一平面的两条直线互相平行;
②分别与两条异面直线都相交的两条直线一定是异面直线;
③若一个平面经过另一个平面的垂线,那么这两个平面相互垂直;
④若两个平面垂直,那么一个平面内与它们的交线不垂直的直线与另一平面也不垂直
其中为真命题的是( )
①平行于同一平面的两条直线互相平行;
②分别与两条异面直线都相交的两条直线一定是异面直线;
③若一个平面经过另一个平面的垂线,那么这两个平面相互垂直;
④若两个平面垂直,那么一个平面内与它们的交线不垂直的直线与另一平面也不垂直
其中为真命题的是( )
| A. | ②和④ | B. | ②和③ | C. | ③和④ | D. | ①和② |
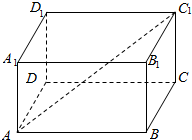 如图,在长方体ABCD-A1B1C1D1中,已知A1A=1,AD=1,AB=$\sqrt{2}$,则体对角线AC1与平面ABCD所成角的大小为30°.
如图,在长方体ABCD-A1B1C1D1中,已知A1A=1,AD=1,AB=$\sqrt{2}$,则体对角线AC1与平面ABCD所成角的大小为30°.