Question

6．某四面体的三视图如图所示，该四面体外接球的表面积为（　　）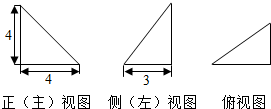

• A． 41π
• B． $\frac{41π}{2}$
• C． 48π
• D． 24π

Answer 1

分析 根据三视图作出四面体的直观图，根据四面体的结构特征寻找外接球的球心位置．计算外接球的半径．

解答 解：作出四面体的直观图如图所示，SA⊥平面ABC，BC⊥AB，其中SA=AB=4，BC=3．
∵∠ABC=90°，∴AC是平面ABC所在截面圆的直径，过AC的中点P作PM⊥平面ABC，交SC于M点，则M为SC的中点，
∵∠SAB=90°，∴SB是平面SAB所在截面圆的直径，过SB的中点N作平面SAB的垂线，显然MN为平面SAB的垂线，
∴M为四面体外接球的球心．
AC=$\sqrt{A{B}^{2}+B{C}^{2}}$=5，∴SC=$\sqrt{S{A}^{2}+A{C}^{2}}$=$\sqrt{41}$．
∴四面体外接球的半径r=$\frac{1}{2}SC$=$\frac{\sqrt{41}}{2}$．
∴四面体外接球的表面积S=4πr²=41π．
故选A．

点评 本题考查了空间几何体的三视图及棱锥的结构特征，棱锥与外接球的关系，属于中档题．