题目内容
14．若函数f（x）=|2x-3|与g（x）=k的图象有且只有两个交点，则实数k的取值范围是0＜k＜3．分析 作出函数f（x）的图象，利用数形结合进行求解即可．
解答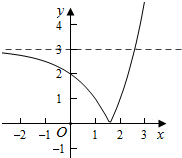 
解：f（x）=|2x-3|=$\left\{\begin{array}{l}{{2}^{x}-3，}&{x≥lo{g}_{2}3}\\{3-{2}^{x}，}&{x＜lo{g}_{2}3}\end{array}\right.$．
则当x＜log23时，f（x）=3-2x∈（0，3），
作出函数f（x）的图象，若f（x）=|2x-3|与g（x）=k的图象有且只有两个交点，
则0＜k＜3；
故答案为：0＜k＜3
点评 本题主要考查函数零点和方程之间的关系，利用数形结合是解决本题的关键．
练习册系列答案
阅读快车系列答案
相关题目
16．$\sqrt{3}$×$\root{3}{\frac{3}{2}}$×$\root{6}{12}$+$\frac{8\sqrt{3}}{3}$×（$\frac{4}{3}$）${\;}^{-\frac{3}{2}}$=（ ）
| A． | 12 | B． | 9 | C． | 6 | D． | 3 |
2．已知函数f（x）是奇函数，且在[0，+∞）上是增函数，不等式f（2x+1）＜f（5）的解集为（ ）
| A． | （2，+∞） | B． | （-∞，2） | C． | [2，+∞） | D． | [3，+∞） |
9．在正方体ABCD-A1B1C1D1中，点O为底面ABCD的中心，点P为线段CC1的中点，则直线OP与平面A1BD所成角的大小为（ ）
| A． | 30° | B． | 45° | C． | 60° | D． | 90° |
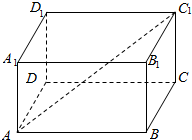如图，在长方体ABCD-A1B1C1D1中，已知A1A=1，AD=1，AB=$\sqrt{2}$，则体对角线AC1与平面ABCD所成角的大小为30°．
如图，椭圆的中心在坐标原点，A，B为顶点，F为焦点，当$\overrightarrow{FB}$⊥$\overrightarrow{AB}$时，此类椭圆称为“黄金椭圆”，可推算出“黄金椭圆”的离心率e=$\frac{\sqrt{5}-1}{2}$．
3．在空间中，“直线a，b没有公共点”是“直线a，b互为异面直线”的（ ）
| A． | 充分而不必要条件 | B． | 必要而不充分条件 | ||
| C． | 充分必要条件 | D． | 既不充分也不必要条件 |