题目内容
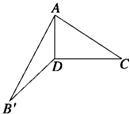如图所示，将等腰直角△ABC沿斜边BC上的高AD折成一个二面角，使得∠B′AC=60°．那么这个二面角大小是（ ）| A、30° | B、60° |
| C、90° | D、120° |
考点：二面角的平面角及求法
专题：空间角
分析：设等腰直角△ABC中AB=AC=a，则BC=
a，B′D=CD=
a，由已知条件推导出∠B′DC是二面角B′-AD-C的平面角．由此能求出二面角B′-AD-C的大小．
| 2 |
| ||
| 2 |
解答：
解：设等腰直角△ABC中AB=AC=a，则BC=
a，
∴B′D=CD=
a，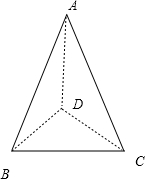
∵等腰直角△ABC斜边BC上的高是AD，
∴B′D⊥AD，CD⊥AD，
∴∠B′DC是二面角B′-AD-C的平面角．
连结B′，C，∵∠B′AC=60°，∴B′C=a，
∴B′D2+CD2=B′C2，
∴∠B′DC=90°．
∴二面角B′-AD-C的大小是90°．
故选：C．
| 2 |
∴B′D=CD=
| ||
| 2 |
∵等腰直角△ABC斜边BC上的高是AD，
∴B′D⊥AD，CD⊥AD，
∴∠B′DC是二面角B′-AD-C的平面角．
连结B′，C，∵∠B′AC=60°，∴B′C=a，
∴B′D2+CD2=B′C2，
∴∠B′DC=90°．
∴二面角B′-AD-C的大小是90°．
故选：C．
点评：本题考查二面角的大小的求法，是中档题，解题时要认真审题，注意空间思维能力的培养．
练习册系列答案
相关题目
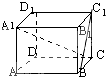如图，长方体ABCD-A1B1C1D1中，AB=AA1=2BC，则直线BC1与直线A1C所成角的余弦值为（ ）A、-
| ||||
B、
| ||||
C、
| ||||
D、
|
正方体的八个顶点共可以连成28条直线，从这28条直线中任取2条直线，这2条直线恰好是一对异面直线．则这样不同的异面直线有多少对（ ）
| A、174 | B、87 |
| C、348 | D、84 |
设数列{an}满足：an+1=an+
，a20=1，则a1=（ ）
| 1 |
| n(n+1) |
A、
| ||
B、
| ||
C、
| ||
D、
|
已知f（x+1）为偶函数，且f（x）在（-∞，1）单调递增，a=f（sin
），b=f（log53），c=f（tan
）则有（ ）
| π |
| 6 |
| π |
| 3 |
| A、a＜b＜c |
| B、b＜c＜a |
| C、c＜b＜a |
| D、c＜a＜b |
复数-2-i（i为虚数单位）在复平面上对应的点在（ ）
| A、第一象限 | B、第二象限 |
| C、第三象限 | D、第四象限 |
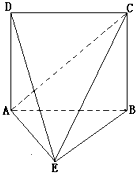如图，四边形ABCD是边长为2的正方形，△ABE为等腰三角形，AE=BE=