题目内容
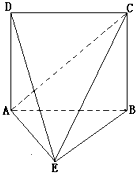 如图,四边形ABCD是边长为2的正方形,△ABE为等腰三角形,AE=BE=
如图,四边形ABCD是边长为2的正方形,△ABE为等腰三角形,AE=BE=| 2 |
(Ⅰ)求证:平面ADE⊥平面BCE;
(Ⅱ)求三棱锥D-ACE的体积.
考点:棱柱、棱锥、棱台的体积,平面与平面垂直的判定
专题:空间位置关系与距离
分析:(Ⅰ)首先,得到AD⊥AB,然后,根据面面垂直,得到AD⊥BE,再借助于直角三角形,得到AE⊥BE,从而得到证明;
(Ⅱ)首先,取AB中点O,然后,借助于VD-ACE=VE-ACD求解.
(Ⅱ)首先,取AB中点O,然后,借助于VD-ACE=VE-ACD求解.
解答:
解:(Ⅰ)∵四边形ABCD是正方形,
∴AD⊥AB.
又∵平面ABCD⊥平面ABE,平面ABCD∩平面ABE=AB,AD?平面ABCD,
∴AD⊥平面ABE,而BE?平面ABE.
∴AD⊥BE.
又∵AE=BE=
,AB=2,
∴AB2=AE2+BE2,∴AE⊥BE
而AD∩AE=A,AD、AE?平面ADE,
∴BE⊥平面ADE 而BE?平面BCE,
∴平面ADE⊥平面BCE.
(Ⅱ)取AB中点O,连接OE.
∵△ABE是等腰三角形,∴OE⊥AB.
又∵平面ABCE⊥平面ABE,平面ABCD∩平面ABE=AB,OE?平面ABCD
∴OE⊥平面ABCD
即OE是三棱锥D-ACE的高.
又∵AE=BE=
AB=2∴OE=1
∴VD-ACE=VE-ACD=
OE•S正方形ABCD=
.
∴AD⊥AB.
又∵平面ABCD⊥平面ABE,平面ABCD∩平面ABE=AB,AD?平面ABCD,
∴AD⊥平面ABE,而BE?平面ABE.
∴AD⊥BE.
又∵AE=BE=
| 2 |
∴AB2=AE2+BE2,∴AE⊥BE
而AD∩AE=A,AD、AE?平面ADE,
∴BE⊥平面ADE 而BE?平面BCE,
∴平面ADE⊥平面BCE.
(Ⅱ)取AB中点O,连接OE.
∵△ABE是等腰三角形,∴OE⊥AB.
又∵平面ABCE⊥平面ABE,平面ABCD∩平面ABE=AB,OE?平面ABCD
∴OE⊥平面ABCD
即OE是三棱锥D-ACE的高.
又∵AE=BE=
| 2 |
∴VD-ACE=VE-ACD=
| 1 |
| 3 |
| 2 |
| 3 |
点评:本题重点考查了空间中垂直关系、空间几何体的体积公式及其运算等知识,属于中档题.

练习册系列答案
相关题目
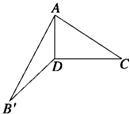 如图所示,将等腰直角△ABC沿斜边BC上的高AD折成一个二面角,使得∠B′AC=60°.那么这个二面角大小是( )
如图所示,将等腰直角△ABC沿斜边BC上的高AD折成一个二面角,使得∠B′AC=60°.那么这个二面角大小是( )| A、30° | B、60° |
| C、90° | D、120° |
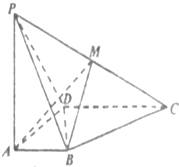 如图所示,四棱锥P-ABCD中,AB⊥AD,CD⊥AD,PA⊥底面ABCD,PA=AD=CD=2AB=2,M为PC的中点.
如图所示,四棱锥P-ABCD中,AB⊥AD,CD⊥AD,PA⊥底面ABCD,PA=AD=CD=2AB=2,M为PC的中点.