题目内容
已知f(x+1)为偶函数,且f(x)在(-∞,1)单调递增,a=f(sin
),b=f(log53),c=f(tan
)则有( )
| π |
| 6 |
| π |
| 3 |
| A、a<b<c |
| B、b<c<a |
| C、c<b<a |
| D、c<a<b |
考点:抽象函数及其应用,函数单调性的性质
专题:函数的性质及应用
分析:本题利用函数的奇偶性,将函数自变量转化到同一单调区间内,再通过自变量的大小比较出函数值的大小,得到本题结论.
解答:
解:∵f(x+1)为偶函数,
∴f(1+x)=f(1-x),
∴y=f(x)关于直线x=1对称.
∴c=f(tan
)=f(
)=f[1+(
-1)]=f[1-(
-1)]=f(2-
),
a=f(sin
)=f(
),
∵3>
,
∴lo
>lo
=
.
∴2-
<
<lo
<1.
∵f(x)在(-∞,1)单调递增,
∴f(2-
)<f(
)<f(lo
).
即c<a<b.
故答案为D.
∴f(1+x)=f(1-x),
∴y=f(x)关于直线x=1对称.
∴c=f(tan
| π |
| 3 |
| 3 |
| 3 |
| 3 |
| 3 |
a=f(sin
| π |
| 6 |
| 1 |
| 2 |
∵3>
| 5 |
∴lo
| g | 3 5 |
| g |
5 |
| 1 |
| 2 |
∴2-
| 3 |
| 1 |
| 2 |
| g | 3 5 |
∵f(x)在(-∞,1)单调递增,
∴f(2-
| 3 |
| 1 |
| 2 |
| g | 3 5 |
即c<a<b.
故答案为D.
点评:本题考查了函数的奇偶性和函数的单调性的应用,考查了化归转化的数学思想.本题思维量不大,但计算略繁,属于中档题.

练习册系列答案
 初中学业考试导与练系列答案
初中学业考试导与练系列答案
相关题目
同时抛掷三枚均匀的硬币,一枚反面朝上,二枚正面朝上的概率等于( )
A、
| ||
B、
| ||
C、
| ||
D、
|
已知函数f(x)=xa的图象过点(4,2),令an=
,n∈N*.记数列{an}的前n项和为Sn,则S2013=( )
| 1 |
| f(n+1)+f(n) |
A、
| ||
B、
| ||
C、
| ||
D、
|
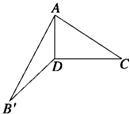 如图所示,将等腰直角△ABC沿斜边BC上的高AD折成一个二面角,使得∠B′AC=60°.那么这个二面角大小是( )
如图所示,将等腰直角△ABC沿斜边BC上的高AD折成一个二面角,使得∠B′AC=60°.那么这个二面角大小是( )| A、30° | B、60° |
| C、90° | D、120° |
若cosα=
(
<α<2π),则cos(α+
)=( )
| ||
| 3 |
| 3π |
| 2 |
| 5π |
| 2 |
A、-
| ||||
B、
| ||||
C、
| ||||
D、-
|