题目内容
设数列{an}满足:an+1=an+
,a20=1,则a1=( )
| 1 |
| n(n+1) |
A、
| ||
B、
| ||
C、
| ||
D、
|
考点:数列递推式
专题:点列、递归数列与数学归纳法
分析:把给出的数列递推式裂项,得到a20=(
-
)+(
-
)+…+(1-
)+a1,整理后代入a20=1求得a1的值.
| 1 |
| 19 |
| 1 |
| 20 |
| 1 |
| 18 |
| 1 |
| 19 |
| 1 |
| 2 |
解答:
解:由an+1=an+
,得:
an+1-an=
-
,
∴a20=(a20-a19)+(a19-a18)+…+(a2-a1)+a1,
即a20=(
-
)+(
-
)+…+(1-
)+a1,
∵a20=1,
∴1=1-
+a1,
则a1=
.
故选:A.
| 1 |
| n(n+1) |
an+1-an=
| 1 |
| n |
| 1 |
| n+1 |
∴a20=(a20-a19)+(a19-a18)+…+(a2-a1)+a1,
即a20=(
| 1 |
| 19 |
| 1 |
| 20 |
| 1 |
| 18 |
| 1 |
| 19 |
| 1 |
| 2 |
∵a20=1,
∴1=1-
| 1 |
| 20 |
则a1=
| 1 |
| 20 |
故选:A.
点评:本题考查数列递推式,考查了裂项法求数列的通项公式,是中档题.

练习册系列答案
 53随堂测系列答案
53随堂测系列答案
相关题目
已知P是双曲线
-
=1(a>0,b>0)的右支上一点,F1,F2分别为双曲线的左、右焦点,双曲线的离心率为e,下列命题正确的是( )
| x2 |
| a2 |
| y2 |
| b2 |
| A、双曲线的焦点到渐近线的距离为a | ||
B、若|PF1|=e|PF2|,则e的最大值为
| ||
| C、△PF1F2的内切圆的圆心的横坐标为b | ||
D、若∠F1PF2的外角平分线交x轴与M,则
|
“x=4”是“x2-4x=0”的( )
| A、充分不必要条件 |
| B、必要不充分条件 |
| C、充分必要条件 |
| D、既不充分也不必要条件 |
已知四棱锥P-ABCD中,底面ABCD是正方形,PA=AD=2,PA⊥平面ABCD,E,F分别是线段AB,BC的中点,则PE与FD所成角的余弦值为( )
A、-
| ||
B、-
| ||
C、
| ||
D、
|
若θ=-5,则角θ的终边在第( )象限.
| A、四 | B、三 | C、二 | D、一 |
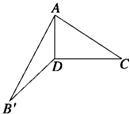 如图所示,将等腰直角△ABC沿斜边BC上的高AD折成一个二面角,使得∠B′AC=60°.那么这个二面角大小是( )
如图所示,将等腰直角△ABC沿斜边BC上的高AD折成一个二面角,使得∠B′AC=60°.那么这个二面角大小是( )| A、30° | B、60° |
| C、90° | D、120° |