题目内容
复数-2-i（i为虚数单位）在复平面上对应的点在（ ）
| A、第一象限 | B、第二象限 |
| C、第三象限 | D、第四象限 |
考点：复数的代数表示法及其几何意义
专题：数系的扩充和复数
分析：直接由复数得到复数-2-i（i为虚数单位）在复平面上对应的点的坐标，则答案可求．
解答：
解：∵复数-2-i（i为虚数单位）在复平面上对应的点的坐标为（-2，-1），
∴复数-2-i（i为虚数单位）在复平面上对应的点在第三象限．
故选：C．
∴复数-2-i（i为虚数单位）在复平面上对应的点在第三象限．
故选：C．
点评：本题考查复数的代数表示法及其几何意义，是基础题．
练习册系列答案
100分闯关期末冲刺系列答案
名校联盟快乐课堂系列答案
相关题目
甲、乙两人从4门课程中各选修1门，则甲、乙所选的课程不相同的选法共有（ ）
| A、6种 | B、12种 |
| C、30种 | D、36种 |
已知四棱锥P-ABCD中，底面ABCD是正方形，PA=AD=2，PA⊥平面ABCD，E，F分别是线段AB，BC的中点，则PE与FD所成角的余弦值为（ ）
A、-
| ||
B、-
| ||
C、
| ||
D、
|
若θ=-5，则角θ的终边在第（ ）象限．
| A、四 | B、三 | C、二 | D、一 |
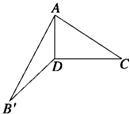如图所示，将等腰直角△ABC沿斜边BC上的高AD折成一个二面角，使得∠B′AC=60°．那么这个二面角大小是（ ）| A、30° | B、60° |
| C、90° | D、120° |
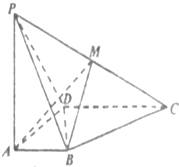如图所示，四棱锥P-ABCD中，AB⊥AD，CD⊥AD，PA⊥底面ABCD，PA=AD=CD=2AB=2，M为PC的中点．