题目内容
“m=1”是“直线x-my+m+1=0与圆x2+y2=2相切”的( )
| A、充分不必要条件 |
| B、必要不充分条件 |
| C、充要条件 |
| D、既不充分也不必要条件 |
考点:必要条件、充分条件与充要条件的判断
专题:直线与圆,简易逻辑
分析:判断是充分条件,还是必要条件,根据充分条件与必要条件的定义即可.而直线与圆是否相切,就看圆心到直线的距离,距离等于圆的半径,则相切,否则不相切.而直线若和圆相切,则圆心到直线的距离等于半径.明白了这些,这道题就容易求解了.
解答:
解:(1)m=1时,直线方程为:x-y+2=0,则圆心(0,0)到这条直线的距离为:
=
,又圆的半径为
,∴直线与圆相切.∴m=1是直线与圆相切的充分条件.
(2)若直线与圆相切,则圆心到直线的距离等于半径,即:
=
,即m2-2m+1=0,∴m=1;
∴m=1是直线与圆相切的必要条件.
综上得出m=1是直线与圆相切的充要条件.
故答案选:C.
| 2 | ||
|
| 2 |
| 2 |
(2)若直线与圆相切,则圆心到直线的距离等于半径,即:
| |m+1| | ||
|
| 2 |
∴m=1是直线与圆相切的必要条件.
综上得出m=1是直线与圆相切的充要条件.
故答案选:C.
点评:而要注意的知识点是,直线和圆相切便得到圆心与直线的距离等于半径;圆心和直线的距离等于半径,便得到相切.还要熟悉的是充分条件和必要条件的定义,点到直线的距离公式,圆的标准方程.

练习册系列答案
相关题目
已知cos(θ+
)=-
,θ∈(0,
),则cos2θ等于( )
| π |
| 4 |
| ||
| 10 |
| π |
| 2 |
A、
| ||
B、-
| ||
C、
| ||
D、-
|
若角α的终边在直线y=-2x上,且sina>0,则cosa值为( )
A、
| ||||
B、-
| ||||
C、-
| ||||
| D、-2 |
已知二面角α-l-β的大小为60°,异面直线m,n分别与α,β垂直,则m,n所成的角为( )
| A、120° | B、90° |
| C、60° | D、30° |
有一段演绎推理是这样的:“若直线平行于平面,则该直线平行于平面内所有直线:已知直线b∥平面α,直线a?平面α,则直线b∥直线a”,结论显然是错误的,这是因为( )
| A、大前提错误 |
| B、小前提错误 |
| C、推理形式错误 |
| D、非以上错误 |
某运动员投篮命中率为0.6,他重复投篮5次,若他命中一次得10分,没命中不得分,命中次数为X,得分为Y,
则EX,DY分别为( )
则EX,DY分别为( )
| A、0.6,60 |
| B、3,12 |
| C、3,120 |
| D、3,1.2 |
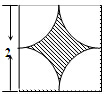 如图所示,墙上挂有边长为2的正方形木板,它的四个角的空白部分都是以正方形的顶点为圆心,半径为1的圆孤,某人向此板投镖,假设每次都能击中木板,且击中木板上每个点的可能性都一样,则它击中阴影部分的概率是( )
如图所示,墙上挂有边长为2的正方形木板,它的四个角的空白部分都是以正方形的顶点为圆心,半径为1的圆孤,某人向此板投镖,假设每次都能击中木板,且击中木板上每个点的可能性都一样,则它击中阴影部分的概率是( )A、
| ||
B、
| ||
C、1-
| ||
D、1-
|
(
-
)n的展开式中只有第5项的二项式系数最大,则展开式中的常数项是( )
| 3 | x |
| 1 |
| x |
| A、28 | B、-28 |
| C、70 | D、-70 |