题目内容
若tan（2π+α）=
，则tan（α+
）=（ ）
| 3 |
| 4 |
| π |
| 4 |
A、
| ||
| B、7 | ||
C、-
| ||
| D、-7 |
考点：运用诱导公式化简求值,同角三角函数基本关系的运用
专题：三角函数的求值
分析：已知等式左边利用诱导公式化简求出tanα的值，原式利用两角和与差的正切函数公式化简后，将tanα的值代入计算即可求出值．
解答：
解：∵tan（2π+α）=tanα=
，
∴tan（α+
）=
=
=7．
故选：B．
| 3 |
| 4 |
∴tan（α+
| π |
| 4 |
| tanα+1 |
| 1-tanα |
| ||
1-
|
故选：B．
点评：此题考查了运用诱导公式化简求值，熟练掌握诱导公式是解本题的关键．
练习册系列答案
千里马走向假期期末仿真试卷寒假系列答案
相关题目
△ABC中，M是BC边的中点，则向量
等于（ ）
| AM |
A、
| ||||||
B、
| ||||||
C、
| ||||||
D、
|
某校共有学生2000名，各年级男、女生人数如右表．已知在全校学生中随机抽取1名，抽到二年级女生的概率是0.19．现用分层抽样的方法在全校抽取80名学生，则应在三年抽取的学生人数为（ ）
| 一年级 | 二年级 | 三年级 | |
| 女生 | 373 | x | y |
| 男生 | 377 | 370 | z |
| A、30 | B、25 | C、24 | D、20 |
在（x2-
）9的二项式展开式中，常数项是（ ）
| 1 |
| x |
| A、504 | B、84 |
| C、-84 | D、-504 |
若
=
，则cosα+sinα=（ ）
| cos2α | ||
cos(
|
| 1 |
| 2 |
A、
| ||||
B、
| ||||
C、
| ||||
D、
|
设等比数列{an}的公比为q，若a8-a4=24，a5-a1=3，则实数q的值为（ ）
| A、3 | ||
| B、2 | ||
C、
| ||
D、
|
设实数x，y满足
则z=
的取值范围是（ ）
|
| 2x+y+2 |
| x+1 |
A、[
| ||
B、[
| ||
C、[1，
| ||
| D、[1，3] |
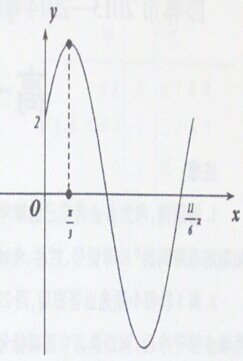已知函数f（x）=Asin（ωx+φ）（ω＞0，0＜φ＜