题目内容
若
=
,则cosα+sinα=( )
| cos2α | ||
cos(
|
| 1 |
| 2 |
A、
| ||||
B、
| ||||
C、
| ||||
D、
|
考点:运用诱导公式化简求值
专题:三角函数的求值
分析:已知等式左边分子利用二倍角的余弦函数公式化简,分母利用两角和与差的余弦函数公式化简,约分即可求出所求式子的值.
解答:
解:∵
=
=
(cosα+sinα)=
,
∴cosα+sinα=
.
故选:D.
| cos2α | ||
cos(
|
| cos2α-sin2α | ||||
|
| 2 |
| 1 |
| 2 |
∴cosα+sinα=
| ||
| 4 |
故选:D.
点评:此题考查了运用诱导公式化简求值,熟练掌握诱导公式是解本题的关键.

练习册系列答案
 阅读快车系列答案
阅读快车系列答案
相关题目
若sinα+2icosα=2i,则α的取值范围为( )
| A、{α|α=kπ,k∈Z} | ||
B、{α|α=
| ||
| C、{α|α=2kπ,k∈Z} | ||
D、{α|α=2kπ+
|
已知集合S={x||x-1|≤2,x∈R},T={x|
≥0,x∈Z},则S∩T=( )
| 5 |
| x+1 |
| A、{x|0<x<3,x∈Z} |
| B、{x|0≤x≤3,x∈Z} |
| C、{x|-1≤x≤3,x∈Z} |
| D、{x|-1<x<3,x∈Z} |
已知Sn为等差数列{an}的前n项和,若a1=-2013,
-
=6,则S2014=( )
| S2010 |
| 2010 |
| S2004 |
| 2004 |
| A、2013 | B、2014 |
| C、0 | D、2 |
若tan(2π+α)=
,则tan(α+
)=( )
| 3 |
| 4 |
| π |
| 4 |
A、
| ||
| B、7 | ||
C、-
| ||
| D、-7 |
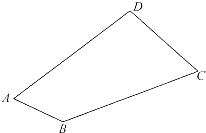 如图,在四边形ABCD中,若∠A=∠C=60°,AD=BC=2,且AB≠CD,则四边形ABCD的面积为( )
如图,在四边形ABCD中,若∠A=∠C=60°,AD=BC=2,且AB≠CD,则四边形ABCD的面积为( )A、
| ||||
B、
| ||||
C、
| ||||
| D、与点B的位置有关 |
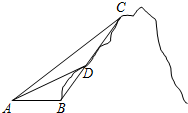 某旅游景点有一座风景秀丽的山峰,游客可以乘长为3km的索道AC上山,也可以沿山路BC上山,山路BC中间有一个距离山脚B为1km的休息点D.已知∠ABC=120°,∠ADC=150°.假设小王和小李徒步攀登的速度为每小时1.2km,请问:两位登山爱好者能否在2个小时内徒步登上山峰(即从B点出发到达C点)
某旅游景点有一座风景秀丽的山峰,游客可以乘长为3km的索道AC上山,也可以沿山路BC上山,山路BC中间有一个距离山脚B为1km的休息点D.已知∠ABC=120°,∠ADC=150°.假设小王和小李徒步攀登的速度为每小时1.2km,请问:两位登山爱好者能否在2个小时内徒步登上山峰(即从B点出发到达C点)